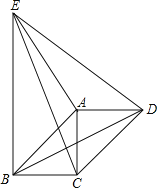
【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
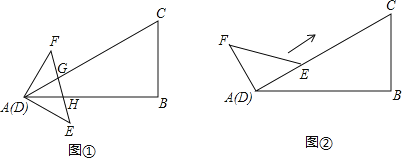
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设![]() ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: ![]() ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动![]() 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 移动到AD=
移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
【解析】试题分析:(1)首先证明△DFG≌△DEH(SAS),进而得出∠FDG=∠EDH,进而得出DF=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,在Rt△DPH中,∠FDG=30°,可得PH′=
|=4x,在Rt△DPH中,∠FDG=30°,可得PH′=![]() DP=2x,由y=S△PDC=
DP=2x,由y=S△PDC=![]() DCPH′求出即可;
DCPH′求出即可;
(2)由(1)知∠FDG=30°,得出∠FDG=∠DCP,以及DP=PC若PH⊥AB则M是DC的中点DM=6,在Rt△DPH中,∠FDG=30°,利用cos∠FDG=![]() 求出AP的长,进而得出x的值;
求出AP的长,进而得出x的值;
(3)分别利用线段AD、FC、BC的长为斜边时求出符合条件的值即可.
试题解析:(1)如图①,过P作PH′⊥AC于H′.
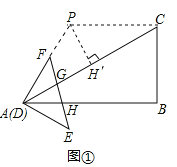
∵DF=DE,
∴∠DFE=∠E
又∵FG=EH,
在△DFG和△DEH中
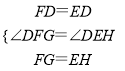 ,
,
∴△DFG≌△DEH(SAS),
∴∠FDG=∠EDH,
∵∠FDE=90°,且∠FDE=∠FDG+∠EDH+∠BAC
∵∠BAC=30°,
∴∠FDG=30°,
∵DF=4,
∴|![]() |=4
|=4
∵![]() =x
=x![]() =x
=x![]() ,
,
∴DP=|![]() |=x|
|=x|![]() |=x|
|=x|![]() |=4x,
|=4x,
在Rt△DPH中,∠FDG=30°,
∴PH′=![]() DP=2x,
DP=2x,
∠B=90°,∠BAC=30°,BC=6,
∴AC=CD=12,
y=S△PDC=![]() DCPH′=
DCPH′=![]() ×122x=12x(x>0);
×122x=12x(x>0);
(2)∵PC∥AB,
∴∠BAC=∠DCP
∵∠BAC=30°,
∴∠DCP=30°,
由(1)知∠FDG=30°,
∴∠FDG=∠DCP,
∴DP=PC
若PH⊥AB,则M是DC的中点DM=6,
在Rt△DPH中,∠FDG=30°,
cos∠FDG=![]() =
=![]() =
=![]() ,
,
∴AP=4![]() ,
,
DP=AP=4x,
∴x=![]() ;
;
(3)如图②,
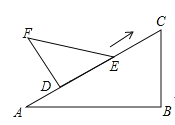
设AD=t,DC=12-t(0<t<12)
FC2=DF2+DC2=42+(12-t)2,
①AD2=FC2+BC2
t2=42+(12-t)2+36
解得:t=![]() (FC至少等于4,故不合题意,舍去)
(FC至少等于4,故不合题意,舍去)
②BC2=FC2+AD2
36=42+(12-t)2+t2,无解,
③FC2=BC2+AD2
∴42+(12-t)2=36+t2
解得t=![]() ,
,
∴当△DEF移动到AD=![]() 时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
A. 沿AE所在直线折叠后,△ACE和△ADE重合
B. 沿AD所在直线折叠后,△ADB和△ADE重合
C. 以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合
D. 以A为旋转中心,把△ACB逆时针旋转270°后与△DAC重合
-
科目: 来源: 题型:
查看答案和解析>>【题目】(发现)
(1)如图1,在ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F.求证:△AOE≌△COF;

(探究)
(2)如图2,在菱形ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F,若AC=4,BD=8,求四边形ABFE的面积.
(应用)
(3)如图3,边长都为1的5个正方形如图摆放,试利用无刻度的直尺,画一条直线平分这5个正方形组成的图形的面积.(要求:保留画图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(方法回顾)
(1)如图1,过正方形ABCD的顶点A作一条直l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .

(问题解决)
(2)如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.
(思维拓展)
(3)如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 .(用含m的式子表示)
-
科目: 来源: 题型:
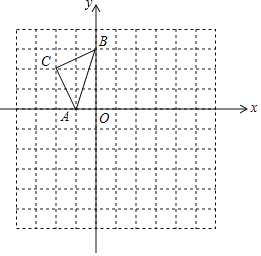
查看答案和解析>>【题目】如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
(1)将△ABC绕原点O顺时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)以点O为位似中心,与△ABC位似的△A2B2C2满足A2B2:AB=2:1,请在网格内画出△A2B2C2,并直接填写△A2B2C2的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材的
 课题学习
课题学习 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠: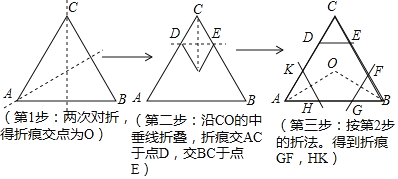
请你根据小明同学的折叠方法,回答以下问题:
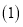 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么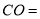 ______
______ 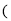 用含a的式子表示
用含a的式子表示 ;
;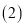 根据折叠性质可以知道
根据折叠性质可以知道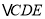 的形状为______ 三角形;
的形状为______ 三角形;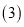 请同学们利用
请同学们利用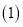 、
、 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形.
相关试题

