【题目】(方法回顾)
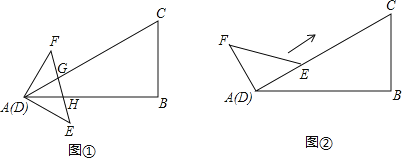
(1)如图1,过正方形ABCD的顶点A作一条直l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .

(问题解决)
(2)如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.
(思维拓展)
(3)如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 .(用含m的式子表示)
参考答案:
【答案】(1)1.5;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)【方法回顾】如图1,利用“![]() ”证明
”证明![]() ,则
,则![]() ,
,![]() ,然后利用
,然后利用![]() 得到
得到![]() .
.
(2)【问题解决】证明![]() ,推出
,推出![]() ,
,![]() ,再利用勾股定理构建方程解决问题即可.
,再利用勾股定理构建方程解决问题即可.
(3)【思维拓展】如图3中,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,设
,设![]() ,
,![]() .设
.设![]() ,由
,由![]() ,推出
,推出![]() ,可得
,可得![]() ,利用勾股定理即可解决问题.
,利用勾股定理即可解决问题.
解:(1)【方法回顾】如图1中,

![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]()
![]() .
.
故答案为1.5.
(2)【问题解决】如图2中,

![]() 四边形
四边形![]() 是菱形,
是菱形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
(3)【思维拓展】如图3中,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,![]() 交
交![]() 的延长线于
的延长线于![]() ,设
,设![]() ,
,![]() .
.

![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]() ,设
,设![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(发现)
(1)如图1,在ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F.求证:△AOE≌△COF;

(探究)
(2)如图2,在菱形ABCD中,点O是对角线的交点,过点O的直线分别交AD,BC于点E,F,若AC=4,BD=8,求四边形ABFE的面积.
(应用)
(3)如图3,边长都为1的5个正方形如图摆放,试利用无刻度的直尺,画一条直线平分这5个正方形组成的图形的面积.(要求:保留画图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△DEF的顶点A与D重合,已知∠B=90°,∠BAC=30°,BC=6,∠FDE=90°,DF=DE=4.
(1)如图①,EF与边AC、AB分别交于点G、H,且FG=EH.设
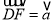 ,在射线DF上取一点P,记:
,在射线DF上取一点P,记: 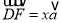 ,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;
,联结CP设△DPC的面积为y,求y关于x的函数解析式,并写出定义域;(2)在(1)的条件下,求当x为何值时PC//AB;
(3)如图②,先将△DEF绕点D逆时针旋转,使点E恰好落在AC边上,在保持DE边与AC边完全重合的条件下,使△DEF沿着AC方向移动
 当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形.
当△DEF移动到什么位置时,以线段AD、FC、BC的长度为边长的三角形是直角三角形. -
科目: 来源: 题型:
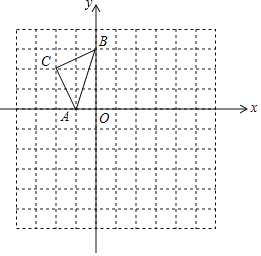
查看答案和解析>>【题目】如图,在已知的平面直角坐标系中,△ABC的顶点都在正方形网格的格点上,若A,B两点的坐标分别是A(-1,0),B(0,3).
(1)将△ABC绕原点O顺时针旋转90°得到△A1B1C1,画出△A1B1C1;
(2)以点O为位似中心,与△ABC位似的△A2B2C2满足A2B2:AB=2:1,请在网格内画出△A2B2C2,并直接填写△A2B2C2的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教材的
 课题学习
课题学习 要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠:
要求同学们用一张正三角形纸片折叠成正六边形,小明同学按照如下步骤折叠: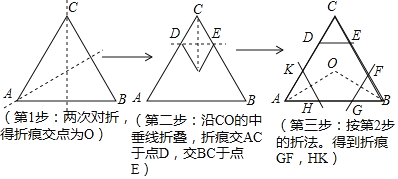
请你根据小明同学的折叠方法,回答以下问题:
 如果设正三角形ABC的边长为a,那么
如果设正三角形ABC的边长为a,那么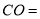 ______
______  用含a的式子表示
用含a的式子表示 ;
; 根据折叠性质可以知道
根据折叠性质可以知道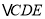 的形状为______ 三角形;
的形状为______ 三角形;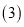 请同学们利用
请同学们利用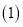 、
、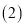 的结论,证明六边形KHGFED是一个六边形.
的结论,证明六边形KHGFED是一个六边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价
 元,
元,(1)降价
 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含 的代数式表示);
的代数式表示);(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
相关试题

