【题目】如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
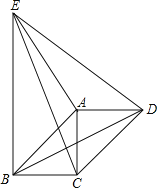
A. 沿AE所在直线折叠后,△ACE和△ADE重合
B. 沿AD所在直线折叠后,△ADB和△ADE重合
C. 以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合
D. 以A为旋转中心,把△ACB逆时针旋转270°后与△DAC重合
参考答案:
【答案】D
【解析】试题解析:A、由于△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,则AD=AC,∠BAC=45°,于是∠EAD=135°,∠CAE=135°,所以△ACE≌△ADE,所以A选项的结论正确;
B、由于△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,则AB=AE,∠BAC=45°,于是∠BAD=135°,∠DAE=135°,所以△ADB≌△ADE,所以B选项的结论正确;
C、由A、B选项得到∠CAD=90°,∠BAE=90°,AB=AE,AD=AC,所以以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合,所以C选项的结论正确;
D、由于四边形ABCD是平行四边形,则△ACB与△DAC为全等的等腰直角三角形,△ACB与△DAC只能经过翻折和平移才能重合,所以D选项的结论错误.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上
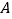 点、
点、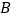 点表示的数分别为
点表示的数分别为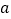 、
、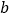 ,则
,则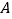 、
、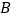 两点之间的距离
两点之间的距离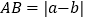 ,线段
,线段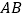 的中点
的中点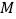 表示的数为
表示的数为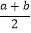 .
.(问题情境)
在数轴上,点
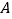 表示的数为-20,点
表示的数为-20,点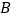 表示的数为10,动点
表示的数为10,动点 从点
从点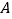 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点 也从点
也从点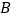 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时, 、
、 两点相遇,且动点
两点相遇,且动点 、
、 运动的速度之比是
运动的速度之比是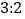 (速度单位:单位长度/秒).
(速度单位:单位长度/秒).

备用图
(综合运用)
(1)点
 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;(2)当
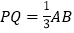 时,求运动时间;
时,求运动时间;(3)若点
 、
、 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点 、
、 的运动,线段
的运动,线段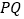 的中点
的中点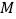 也随着运动.问点
也随着运动.问点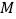 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从 、
、 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点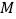 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种数量与3月份相同,4月份共收取运费13000元.试求该物流公司月运输A、B两种货物各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.
(1)补全频数分布直方图;
(2)扇形图中m=;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人? -
科目: 来源: 题型:
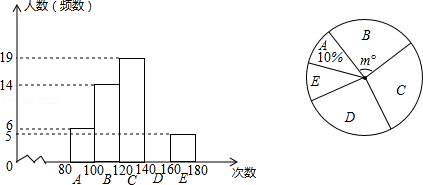
查看答案和解析>>【题目】请仅用无刻度的直尺在下列图1和图2中按要求画菱形.
(1)图1是矩形ABCD,E,F分别是AB和AD的中点,以EF为边画一个菱形;
(2)图2是正方形ABCD,E是对角线BD上任意一点(BE>DE),以AE为边画一个菱形. -
科目: 来源: 题型:
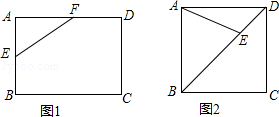
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
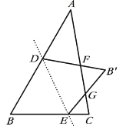
查看答案和解析>>【题目】如图,△ABC 中,∠B=60°,∠C=80°,点D,E分别在线段AB,BC 上, 将△BDE 沿直线DE翻折,使B落在B′ 处, B′ D, B′E分别交AC于F,G. 若∠ADF=70°,则∠CGE 的度数为______.
相关试题

