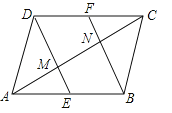
【题目】如图,在ABCD中,E、F分别是AB、CD的中点.
(1)求证:四边形EBFD为平行四边形;
(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.
参考答案:
【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】
试题分析:(1)根据平行四边形的性质,得到AB∥CD,AB=CD;再根据一组对边平行且相等的四边形是平行四边形,可得答案;
(2)根据平行四边的性质,可得AB∥CD,AB=CD,∠CDM=∠CFN;根据全等三角形的判定,可得答案.
试题解析:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∵E、F分别是AB、CD的中点,∴BE=DF,∵BE∥DF,∴四边形EBFD为平行四边形;
(2)∵四边形EBFD为平行四边形,∴DE∥BF,∴∠CDM=∠CFN,∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠BAC=∠DCA,∠ABN=∠CFN,∴∠ABN=∠CDM,在△ABN与△CDM中,∵∠BAN=∠DCM,AB=CD,∠ABN=∠CDM,∴△ABN≌△CDM (ASA).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,

(1)请画出平移后的图形△A′B′C′;
(2)并写出△A′B′C′各顶点的坐标;
(3)求出△A′B′C′的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a3a2=a6
B.(a2)2=a4
C.(﹣3a)3=﹣9a3
D.a4+a5=a9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形
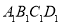 的边长为2,
的边长为2,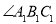 =60°,对角线
=60°,对角线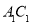 ,
,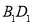 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以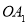 ,
,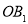 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以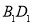 为对角线作菱形
为对角线作菱形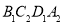 ∽菱形
∽菱形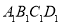 ,再以
,再以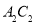 为对角线作菱形
为对角线作菱形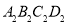 ∽菱形
∽菱形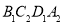 ,再以
,再以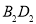 为对角线作菱形
为对角线作菱形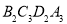 ∽菱形
∽菱形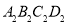 ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点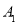 ,
,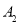 ,
,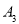 ,......,
,......,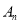 ,则点
,则点 的坐标为________.
的坐标为________.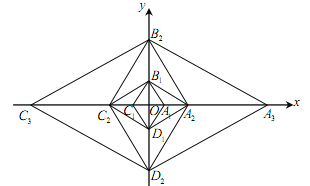
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3a=5,3b=10,则3a+b的值是( )
A.10
B.20
C.50
D.40 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x2+y2)(x2+y2﹣4)=5,则x2+y2的值为( )
A.1B.﹣1或5C.5D.1或﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
相关试题

