【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣ ![]() ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 ![]() PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
参考答案:
【答案】
(1)
解:由题意 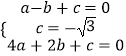 解得
解得 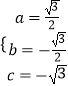 ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∵y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() =
= ![]() (x﹣
(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴顶点坐标( ![]() ,﹣
,﹣ ![]() )
)
(2)![]()
(3)
① 5
②解:如图,RT△AOB中,∵tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,
以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.
则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,
∵EB= ![]() =
= ![]() ,
,
∴OE=OB﹣EB= ![]() ,
,
∵F( ![]() ,t),EF2=EB2,
,t),EF2=EB2,
∴( ![]() )2+(t+
)2+(t+ ![]() )2=(
)2=( ![]() )2,
)2,
解得t= ![]() 或
或 ![]() ,
,
故F( ![]() ,
, ![]() ),G(
),G( ![]() ,
, ![]() ),
),
∴t的取值范围 ![]() ≤t≤
≤t≤ ![]()
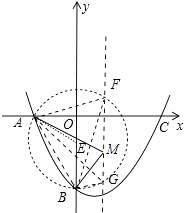
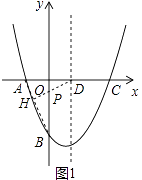
【解析】【解析】解:(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,
此时 ![]() PB+PD最小.
PB+PD最小.
理由:∵OA=1,OB= ![]() ,
,
∴tan∠ABO= ![]() =
= ![]() ,
,
∴∠ABO=30°,
∴PH= ![]() PB,
PB,
∴ ![]() PB+OD=PH+PD=DH,
PB+OD=PH+PD=DH,
∴此时 ![]() PB+PD最短(垂线段最短).
PB+PD最短(垂线段最短).
在RT△ADH中,∵∠AHD=90°,AD= ![]() ,∠HAD=60°,
,∠HAD=60°,
∴sin60°= ![]() ,
,
∴DH= ![]() ,
,
∴ ![]() PB+PD的最小值为
PB+PD的最小值为 ![]() .
.
所以答案是 ![]() .
.
(3)①以A为圆心AB为半径画弧与对称轴有两个交点,
以B为圆心AB为半径画弧与对称轴也有两个交点,
线段AB的垂直平分线与对称轴有一个交点,
所以满足条件的点M有5个,即满足条件的点N也有5个,
所以答案是5.
(1)利用待定系数法转化为解方程组解决问题.(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,此时 ![]() PB+PD最小.最小值就是线段DH,求出DH即可.(3)①先在对称轴上寻找满足△ABM是等腰三角形的点M,由此即可解决问题.②作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,求出F、G的坐标即可解决问题.本题考查二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用垂线段最短解决实际问题中的最短问题,学会添加辅助线,构造圆解决角度问题,属于中考压轴题.
PB+PD最小.最小值就是线段DH,求出DH即可.(3)①先在对称轴上寻找满足△ABM是等腰三角形的点M,由此即可解决问题.②作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,求出F、G的坐标即可解决问题.本题考查二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用垂线段最短解决实际问题中的最短问题,学会添加辅助线,构造圆解决角度问题,属于中考压轴题.
【考点精析】根据题目的已知条件,利用垂线段最短和锐角三角函数的增减性的相关知识可以得到问题的答案,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;当角度在0°~90°之间变化时:(1)正弦值随着角度的增大(或减小)而增大(或减小)(2)余弦值随着角度的增大(或减小)而减小(或增大)(3)正切值随着角度的增大(或减小)而增大(或减小)(4)余切值随着角度的增大(或减小)而减小(或增大).
-
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:
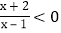 ;
;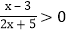 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:(1)若
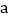 >0,
>0,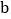 >0,则
>0,则 >0;若
>0;若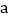 <0,
<0,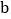 <0,则
<0,则 >0;
>0;(2)若
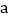 >0,
>0,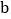 <0,则
<0,则 <0;若
<0;若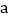 <0,
<0,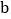 >0,则
>0,则 <0.
<0.反之:(1)若
 >0,则
>0,则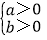 或
或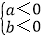
(2)若
 <0,则__________或__________.
<0,则__________或__________.(3)根据上述规律,求不等式
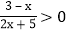 的解集.
的解集.(4)试求不等式
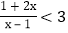 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N

(1)若CM=x,则CH=(用含x的代数式表示);
(2)求折痕GH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O是平行四边形ABCD两条对角线的交点,点P是AC所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线BP作垂线,垂足分别为E、F
(1)如图1,当点P与点O重合时,求证:OE=OF
(2)直线BP绕点B逆时针方向旋转,当∠OFE=
 时,有OE=OF,如图2,线段CF、AE、OE之间有怎样的数量关系?给出证明。
时,有OE=OF,如图2,线段CF、AE、OE之间有怎样的数量关系?给出证明。(3)当点P在图3位置,且∠OFE=
 时,线段CF、AE、OE之间有怎样的数量关系?(直接写出结论,无需证明.
时,线段CF、AE、OE之间有怎样的数量关系?(直接写出结论,无需证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
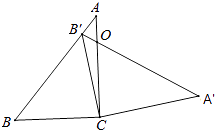
A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市某学校对学生的上学方式进行抽样调查,A类学生骑共享单车,B类学生坐公交车,私家车,C类学生步行,D类学生用其他方式,根据调查结果绘制了完整的统计图
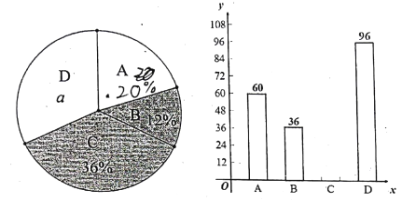
(1)样本容量_____________,a=_________。
(2)补全条形统计图。
(3)若该校有3000人,则骑共享单车的有多少人?
相关试题

