搜索
【题目】如图，将矩形
沿直线
折叠，顶点
恰好落在
边上
点处，已知
，则图中阴影部分面积为（ ）
A.
B.
C.
D.
参考答案：
【答案】C
【解析】
根据折叠的性质求出DE＝EF＝5，在Rt△CEF中，利用勾股定理求出CF＝4，设AD＝x，则AD＝AF＝BC＝x，在Rt△ABF中，利用勾股定理构建方程即可解决问题．
解：设AD＝x，则AD＝AF＝BC＝x，
∵AB＝8，
∴CD＝AB＝8，
∵CE＝3，
∴EF＝DE＝CD﹣CE＝8﹣3＝5，
在直角△CEF中，CF＝
＝4，
∴BF＝x﹣4，
在直角△ABF中，AB2+BF2＝AF2，即64+（x﹣4）2＝x2，
解得：x＝10，
∴S△ADE＝S△AFE＝
ADDE＝×10×5＝25，
∵S矩形ABCD＝10×8＝80，
∴S阴影＝S矩形ABCD﹣S△ADE﹣S△AFE＝80﹣25﹣25＝30．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线
与直线
交于
，
两点，点
是抛物线上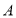
，之间的一个动点，过点分别作
轴、
轴的平行线与直线
交于点
，
.
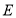（1）求抛物线的解析式；
（2）若
为的中点，求
的长；（3）如图，以
，
为边构造矩形
，设点
的坐标为
，①请求出
，
之间的关系式；②求出矩形的周长最大时，点的坐标. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：在Rt△ABC中，∠C=90°，BC=1，AC=
，点D是斜边AB的中点，点E是边AC上一点，则DE+BE的最小值为（ ）
A. 2
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，直线AB和CD与直线MN相交.
（1）如图①，EG平分∠BEF，FH平分∠DFE(平分的是一对同旁内角)，则∠1与∠2满足________时，AB∥CD；
（2）如图②，EG平分∠MEB，FH平分∠DFE(平分的是一对同位角)，则∠1与∠2满足________时，AB∥CD；
（3）如图③，EG平分∠AEF，FH平分∠DFE(平分的是一对内错角)，则∠1与∠2满足什么条件时，AB∥CD？请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将三角形向右平移3个单位长度，再向上平移2个单位长度，则平移后三个顶点的坐标为（ ）
A.（-1，-1），（2，3），（5，1）
B.（-1，1），（3，2），（5，1）
C.（-1，1），（2，3），（5，1）
D.（1，-1），（2，2），（5，1） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、B（2，2）、C（2，1），D（3，3）．
（1）以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；
（2）在（1）的前提下，写出点A的对应点坐标A′，并说明点A与点A′坐标的关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校为美化校园，计划对某一区域进行绿化，安排甲．乙 两个工程队完成；已知甲队每天能完成绿化面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为400
区域的绿化时，甲队比乙队少用4天，求甲．乙两工程队每天能完成绿化的面积分别是多少．
相关试题
