【题目】已知:在Rt△ABC中,∠C=90°,BC=1,AC=![]() ,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )
,点D是斜边AB的中点,点E是边AC上一点,则DE+BE的最小值为( )

A. 2
B. ![]()
C. ![]()
D. ![]()
参考答案:
【答案】C
【解析】
作B关于AC的对称点B',连接B′D,易求∠ABB'=60°,则AB=AB',且△ABB'为等边三角形,BE+DE=DE+EB'为B'与直线AB之间的连接线段,其最小值为B'到AB的距离=AC=![]() ,所以最小值为
,所以最小值为![]() .
.
解:作B关于AC的对称点B',连接B′D,

∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°,
∵AB=AB',
∴△ABB'为等边三角形,
∴BE+DE=DE+EB'为B'与直线AB之间的连接线段,
∴最小值为B'到AB的距离=AC=![]() ,
,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点
 、
、 ,连接
,连接 .如果点
.如果点 在直线
在直线 上,且点
上,且点 到直线
到直线 的距离不大于1,那么称点
的距离不大于1,那么称点 是线段
是线段 的“临近点”.
的“临近点”.
(1)判断点
 是否是线段
是否是线段 的“临近点”,并说明理由;
的“临近点”,并说明理由;(2)若点
 是线段
是线段 的“临近点”.①求
的“临近点”.①求 的取值范围;②设直线
的取值范围;②设直线 与
与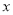 轴交于
轴交于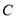 点,试用
点,试用 表达
表达 的面积
的面积 ,并求出
,并求出 的最大面积.
的最大面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学新建了一栋7层的教学大楼,每层楼有8间教室,进出这栋大楼共有八道门,其中四道正门大小相同,四道侧门大小也相同.安全检查中,对八道门进行了测试:当同时开启一道正门和两道侧门时,2分内可以通过560名学生;当同时开启一道正门和一道侧门时,4分内可以通过800名学生.
(1)平均每分内一道正门和一道侧门分别可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低30%.安全检查规定:在紧急情况下全大楼的学生应在5分内通过这八道门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问建造的这八道门是否符合安全规定?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与直线
与直线 交于
交于 ,
, 两点,点
两点,点 是抛物线上
是抛物线上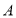 ,
, 之间的一个动点,过点
之间的一个动点,过点 分别作
分别作 轴、
轴、 轴的平行线与直线
轴的平行线与直线 交于点
交于点 ,
,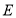 .
.
(1)求抛物线的解析式;
(2)若
 为
为 的中点,求
的中点,求 的长;
的长;(3)如图,以
 ,
, 为边构造矩形
为边构造矩形 ,设点
,设点 的坐标为
的坐标为 ,
,①请求出
 ,
, 之间的关系式;②求出矩形
之间的关系式;②求出矩形 的周长最大时,点
的周长最大时,点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线AB和CD与直线MN相交.
(1)如图①,EG平分∠BEF,FH平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足________时,AB∥CD;
(2)如图②,EG平分∠MEB,FH平分∠DFE(平分的是一对同位角),则∠1与∠2满足________时,AB∥CD;
(3)如图③,EG平分∠AEF,FH平分∠DFE(平分的是一对内错角),则∠1与∠2满足什么条件时,AB∥CD?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形
 沿直线
沿直线 折叠,顶点
折叠,顶点 恰好落在
恰好落在 边上
边上 点处,已知
点处,已知 ,则图中阴影部分面积为( )
,则图中阴影部分面积为( ) 
A.
 B.
B.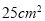 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将三角形向右平移3个单位长度,再向上平移2个单位长度,则平移后三个顶点的坐标为( )

A.(-1,-1),(2,3),(5,1)
B.(-1,1),(3,2),(5,1)
C.(-1,1),(2,3),(5,1)
D.(1,-1),(2,2),(5,1)
相关试题

