【题目】如图，二次函数y=x2+bx+c的图象交x轴于A、B两点，交y轴于点C，顶点为点P，经过B、C两点的直线为y=﹣x+3．

（1）求该二次函数的关系式；

（2）在该抛物线的对称轴上是否存在点M，使以点C、P、M为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的点M的坐标；若不存在，请说明理由；

（3）连接AC，在x轴上是否存在点Q，使以点P、B、Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）二次函数解析式为y=x2-4x+3．（2）M1（2，7），M2（2，2-1），M3（2， ），M4（2，-2-1）；（3）存在点Q使得以点P、B、Q为顶点的三角形与△ABC相似．点Q坐标（0，0）或（，0）．

【解析】试题分析：（1）先求出B、C坐标，代入抛物线解析式解方程组即可解决问题．

（2）分三种情形讨论即可①CM=CP，②PM=PC，③MP=MC，画出图形即可解决问题．

（3）分两种情形讨论即可①时，△ABC∽△PBQ1，列出方程即可解决．②当时，△ABC∽△Q2BP，列出方程即可解决．

试题解析：（1）∵直线y=-x+3经过B、C两点，

∴B（3，0），C（0，3），

∵二次函数y=x2+bx+c图象交x轴于A、B两点，交y轴于点C，

∴解得，

∴二次函数解析式为y=x2-4x+3．

（2）∵y=x2-4x+3=（x-2）2-1，

∴该抛物线的对称轴为直线x=2，顶点坐标为P（2，-1），

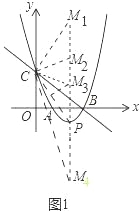
∴如图1所示，满足条件的点M分别为

M1（2，7），M2（2，2-1），M3（2， ），M4（2，-2-1）．

（3）由（1）（2）得A（1，0），BP=，BC=3，AB=2，

如图2所示，连接BP，∠CBA=∠ABP=45°，

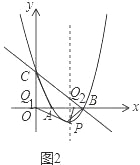
①时，△ABC∽△PBQ1，

此时，

∴BQ1=3，

∴Q1（0，0）．

②当时，△ABC∽△Q2BP，

此时， ，

∴BQ2=，

∴Q2（，0），

综上所述，存在点Q使得以点P、B、Q为顶点的三角形与△ABC相似．点Q坐标（0，0）或（，0）．

关闭