【题目】如图,点![]() 是直线
是直线![]() 与
与![]() 的交点,点
的交点,点![]() 在
在![]() 上,
上, ![]() 垂足为
垂足为![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 平分
平分![]() .
.
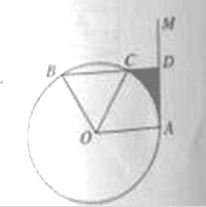
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求图中阴影部分的面积(结果保留
,求图中阴影部分的面积(结果保留![]() 和根号).
和根号).
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)由已知条件得到△BOC是等边三角形,根据等边三角形的性质得到∠1=∠2=60°,由角平分线的性质得到∠1=∠3,根据平行线的性质得到∠OAM=90°,于是得到结论;
(2)根据等边三角形的性质得到∠OAC=60°,根据三角形的内角和得到∠CAD=30°,根据勾股定理得到AD=2![]() ,于是得到结论.
,于是得到结论.
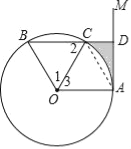
试题解析:(1)∵∠B=60°,∴△BOC是等边三角形,∴∠1=∠2=60°,
∵OC平分∠AOB,∴∠1=∠3,∴∠2=∠3,∴OA∥BD,
∴∠BDM=90°,∴∠OAM=90°,∴AM是⊙O的切线;
(2)∵∠3=60°,OA=OC,∴△AOC是等边三角形,
∴∠OAC=60°,∵∠OAM=90°,∴∠CAD=30°,
∵CD=2,∴AC=2CD=4,∴AD=2![]() ,
,
∴S阴影=S梯形OADC﹣S扇形OAC=![]() (4+2)×2
(4+2)×2![]() ﹣
﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A. 形状相同的两个图形是全等形
B. 对应角相等的两个三角形是全等三角形
C. 全等三角形的面积相等
D. 两个等边三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.a3+a3=2a6
B.a5﹣a3=a2
C.a2a2=2a4
D.(a5)2=a10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,设
中,设 的对边分别为
的对边分别为 ,过点
,过点 作
作 ,垂足为
,垂足为 ,会有
,会有 ,则
,则
 ,即
,即
同理
 ,
,
通过推理还可以得到另一个表达三角形边角关系的定理—余弦定理:

在
 中,若
中,若 的对边分别为
的对边分别为 ,则
,则


用上面的三角形面积公式和余弦定理解决问题:
(1)如图,在
 中,
中, ,
, 的对边分别是3和8.
的对边分别是3和8.
求
 和
和 .
.解:
 _______________;
_______________; ______________.
______________.(2)在
 中,已知
中,已知 ,
, 分别是以
分别是以 为边长的等边三角形,设
为边长的等边三角形,设 的面积分别为
的面积分别为 ,求证:
,求证:  .
.
-
科目: 来源: 题型:
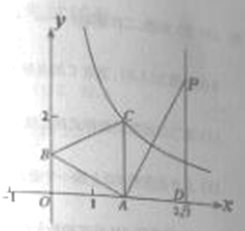
查看答案和解析>>【题目】如图,一次函数
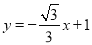 的图象与
的图象与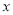 轴、
轴、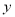 轴分别交于点
轴分别交于点 ,以线段
,以线段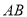 为边在第一象限作等边
为边在第一象限作等边 .
.
(1)若点
 在反比例函数
在反比例函数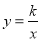 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;(2)点
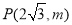 在第一象限,过点
在第一象限,过点 作
作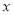 轴的垂线,垂足为
轴的垂线,垂足为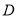 ,当
,当 与
与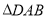 相切时,
相切时, 点是否在(1)中反比例函数图象上,如果在,求出
点是否在(1)中反比例函数图象上,如果在,求出 点坐标;如果不在,请加以说明.
点坐标;如果不在,请加以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】上海市2018年有77所民办小学进行招生,共计招生1.4万人,这里的1.4万精确到_______位.
-
科目: 来源: 题型:
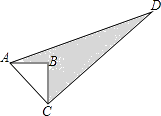
查看答案和解析>>【题目】如图,△ABC中,∠B=90°,AB=3,BC=4,若CD=12,AD=13.求阴影部分的面积.
相关试题

