【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.



(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
参考答案:
【答案】(Ⅰ)∠DAO=60°,DE=2; (Ⅱ)①GH=6,DG=﹣3+![]() ;②F(﹣5﹣
;②F(﹣5﹣![]() ,0).
,0).
【解析】解:(Ⅰ)∵A(﹣2,0),D(0,2![]() )∴AO=2,DO=2
)∴AO=2,DO=2![]() ,∴tan∠DAO=
,∴tan∠DAO=![]() =
=![]() ,
,
∴∠DAO=60°,∴∠ADO=30°,∴AD=2AO=4,∵点E为线段AD中点,∴DE=2;
(Ⅱ)①如图2,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,∴AD∥OF′,∴∠OF′E=∠DEH,∴∠DEH=∠DGE,
∵∠DEH=∠EDG,∴△DHE∽△DEG,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DG=x,则DH=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,∴DG=﹣3+
,∴DG=﹣3+![]() .
.
②如图3,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,∴∠EOF′=∠AEO,∴AD∥OF′,
∴∠OF′E=∠DEH,∴∠DEG=∠DHE,
∵∠DEG=∠EDH,∴△DGE∽△DEH,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DH=x,则DG=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,
,
∴DH=﹣3+![]() .∴DG=3+
.∴DG=3+![]() ∴DG=AF=3+
∴DG=AF=3+![]() ,∴OF=5+
,∴OF=5+![]() ,∴F(﹣5﹣
,∴F(﹣5﹣![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
证明:∵∠1=∠2(_________),∠1=∠3 ,∠2=∠4(_____________),
∴∠3=∠4(_________).
∴____________∥____________(_______________).
∴∠C=∠ABD(_____________).
∵∠C=∠D(__________),
∴∠D=________(____________).
∴AC∥DF(_____________).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果代数式x+2y的值是5,则代数式2x+4y+8的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:
 ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:  是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取 =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.

-
科目: 来源: 题型:
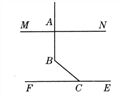
查看答案和解析>>【题目】如图,已知MN⊥AB,∠ABC=130°,∠FCB=40°,试判断直线MN与EF的位置关系,并说明理由.(至少用两种方法说明)
相关试题

