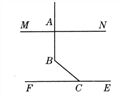
【题目】如图,已知MN⊥AB,∠ABC=130°,∠FCB=40°,试判断直线MN与EF的位置关系,并说明理由.(至少用两种方法说明)

参考答案：

【答案】见解析

【解析】试题分析：MN∥EF， 方法一：延长AB交EF于点D，通过三角形内角和求得∠BDC=90°再由已知求得∠1=90°，从而得∠1=∠BDC，从而得证；

方法二：过点B作直线PQ∥EF， 由已知可证明MN∥PQ，从而得证.

试题解析：MN∥EF，理由如下：

方法一：如图，延长AB交EF于点D，

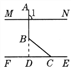
∵∠ABC=130°，∴∠DBC=180°-130°=50°，

∵∠FCB=40°，∠BDC+∠CBD+∠FCB=180°，

∴∠BDC=90°，∵MN⊥AB，∴∠1=90°，

∴∠1=∠BDC，∴MN∥EF；

方法二：过点B作直线PQ∥EF，如图所示，

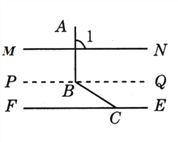
∵PQ∥EF，∴∠CBQ=∠FCB=40°，

∵∠ABC=130°，∴∠ABQ=90°，

∵MN⊥AB，∴∠1=90°，

∴∠1=∠ABQ，∴MN∥PQ，

又∵PQ∥EF，∴MN∥EF.

关闭