搜索
【题目】如图△ABC中，点D是边AB的中点，CE∥AB，且AB=2CE，连结BE、CD。
（1）求证：四边形BECD是平行四边形；
（2）用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)
参考答案：
【答案】（1）证明见解析 （2）答案见解析
【解析】
（1）利用线段中点的定义可证得AB=2BD，再结合已知证明BD=CE，然后利用有一组对边平行且相等的四边形是平行四边形，可得结论；
（2）连接DE交BC于点G ，连接AG，利用平行四边形的对角线互相平分，可得点G时BC的中点，利用三角形的中线的定义，可知AG是中线.
（1）解： ∵点D是边AB的中点，
∴AB=2BD，
∵AB=2CE，
∴BD=CE；
∵CE∥AB
∴四边形BECD是平行四边形。
（2）解： 连接DE交BC于点G ，连接AG，
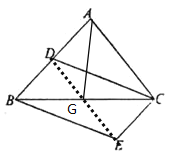
∵四边形BECD是平行四边形，
∴BG=CG，
∴AG是△ABC的BC边上的中线，
即AG就是所求作的图形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，四边形ABCD中，AB∥CD，AB=8，DC=4，点M、N分别为边AB、DC的中点，点P从点D出发，以每秒1个单位的速度从D→C方向运动，到达点C后停止运动，同时点Q从点B出发，以每秒3个单位的速度从B→A方向运动，到达点A后立即原路返回，点P到达点C后点Q同时停止运动，设点P、Q运动的时问为t秒，当以点M、N、P、Q为顶点的四边形为平行四边形时，t的值为________。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一次函数图像过点P(0，6)，且平行于直线y=-2x
（1）求该一次函数的解析式
（2）若点A(
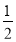，a)、B(2，b)在该函数图像上，试判断a、b的大小关系，并说明理由。 -
科目： 来源： 题型：
查看答案和解析>>【题目】某检修小组乘一辆汽车沿公路东西方向检修线路，约定向东为正，某天从A地出发到收工时行走记录为（单位：千米）：
+15、—2、+5、—1、—3、—2、+4、—5
（1）计算收工时，检修小组在A地的哪一边，距A地多远？
（2）若每千米汽车耗油量为0.4升，求出发到收工检修小组耗油多少升？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上有两点A、B，点A表示的数是4，点B表示的数是﹣11，点C是数轴上一动点．
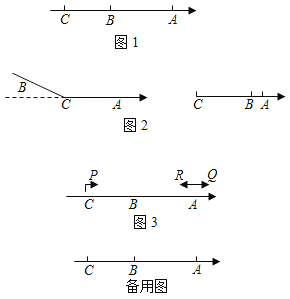
（1）如图1，若点C在点B的左侧，且BC：AB＝3：5，求点C到原点的距离．
（2）如图2，若点C在A、B两点之间时，以点C为折点，将此数轴向右对折，当A、B两点之间的距离为1时，求C点在数轴上对应的数是多少？
（3）如图3，在（1）的条件下，动点P、Q两点同时从C、A出发向右运动，同时动点R从点A向左运动，已知点P的速度是点R的速度的3倍，点Q的速度是点R的速度的2倍少5个单位长度/秒．经过4秒，点P、Q之间的距离是点Q、R之间距离的一半，求动点Q的速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC，按如下步骤作图：
①分别以A，C为圆心，大于
的长为半径画弧，两弧交于P，Q两点； ②作直线PQ，分别交AB，AC于点E，D，连接CE；
③过C作CF∥AB交PQ于点F，连接AF．
（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】经过建设者三年多艰苦努力地施工，贯通我市A、B两地又一条高速公路全线通车．已知原来A地到B地普通公路长150km，高速公路路程缩短了30km，如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍，需要的时间可以比原来少用1小时．求小车走普通公路的平均速度是多少？
相关试题
