【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由作图知:PQ为线段AC的垂直平分线,从而得到AE=CE,AD=CD,然后根据CF∥AB得到∠EAC=∠FCA,∠CFD=∠AED,利用ASA证得两三角形全等即可;
(2)根据全等到AE=CF,然后根据EF为线段AC的垂直平分线,得到EC=EA,FC=FA,从而得到EC=EA=FC=FA,利用四边相等的四边形是菱形判定四边形AECF为菱形
试题解析:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
 ,
,
∴△AED≌△CFD;
(2)∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个多边形的内角和是它的外角和的2倍,那么这个多边形的边数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“相似的图形”是( )
A.形状相同的图形
B.大小不相同的图形
C.能够重合的图形
D.大小相同的图形 -
科目: 来源: 题型:
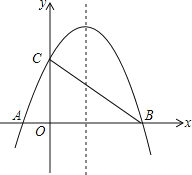
查看答案和解析>>【题目】如图,已知抛物线y=﹣
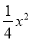 +bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
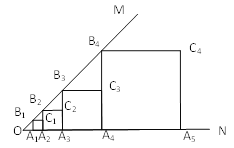
查看答案和解析>>【题目】如上图,已知∠MON=45,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4……在射线ON上,点B1、B2、B3、B4……在射线OM上,依此类推,则第6个正方形的面积S6=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】36.36°=______ (用度、分、秒表示,下同);36.36°的补角的度数为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式15a3b2(a+b)c+10a2b(a+b)的公因式是( )
A.5a3b2(a+b)
B.a2b(a+b)
C.5ab(a+b)
D.5a2b(a+b)
相关试题

