【题目】已知,四边形ABCD中,AB∥CD,AB=8,DC=4,点M、N分别为边AB、DC的中点,点P从点D出发,以每秒1个单位的速度从D→C方向运动,到达点C后停止运动,同时点Q从点B出发,以每秒3个单位的速度从B→A方向运动,到达点A后立即原路返回,点P到达点C后点Q同时停止运动,设点P、Q运动的时问为t秒,当以点M、N、P、Q为顶点的四边形为平行四边形时,t的值为________。

参考答案:
【答案】1或1.5或3.5
【解析】
利用线段中点的定义求出DN,BM的长,再根据两点的运动速度及运动方向,分情况讨论:当0<t≤2时,PN=2-t,MQ=4-3t或MQ=3t-4;当2<t≤4时PN=t-2,MQ=12-3t,然后根据平行四边形的判定定理,由题意可知当PN=MQ,以点M、N、P、Q为顶点的四边形为平行四边形,分别建立关于t的方程,分别求解即可
解:∵点M、N分别为边AB、DC的中点,
∴DN=![]() DC=
DC= ![]() ×4=2,
×4=2,
BM=![]() AB=
AB=![]() ×8=4;
×8=4;
∵点P从点D出发,以每秒1个单位的速度从D→C方向运动,到达点C后停止运动,同时点Q从点B出发,以每秒3个单位的速度从B→A方向运动,点P到达点C后点Q同时停止运动,
∴DP=t,BQ=3t,
当0<t≤2时,PN=2-t,MQ=4-3t或MQ=3t-4
当2<t≤4时PN=t-2,MQ=12-3t
∵ AB∥CD
∴PN∥MQ;
∴当PN=MQ,以点M、N、P、Q为顶点的四边形为平行四边形,
∴2-t=4-3t,或2-t=3t-4,或t-2=12-3t,
解之:t=1或t=1.5或t=3.5.
故答案为:t=1或1.5或3.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
【答案】(1)2400元;(2)8台.
【解析】试题分析:(1)设商场第一次购入的空调每台进价是x元,根据题目条件“商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,每台的售价也上调了200元”列出分式方程解答即可;
(2)设最多将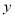 台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.
台空调打折出售,根据题目条件“在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售”列出不等式并解答即可.试题解析:(1)设第一次购入的空调每台进价是x元,依题意,得
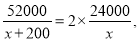 解得
解得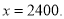
经检验,
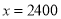 是原方程的解.
是原方程的解.答:第一次购入的空调每台进价是2 400元.
(2)由(1)知第一次购入空调的台数为24 000÷2 400=10(台),第二次购入空调的台数为10×2=20(台).
设第二次将y台空调打折出售,由题意,得
 解得
解得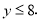
答:最多可将8台空调打折出售.
【题型】解答题
【结束】
23【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: AB·BH=2BG·EH
(2)若∠CGF=90°,
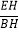 =3时,求
=3时,求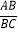 的值.
的值.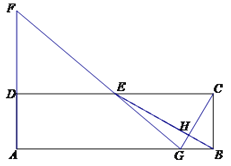
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①2a+b=0;②abc<0;③b2﹣4ac>0;④8a+c>0.其中正确的有( )
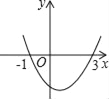
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
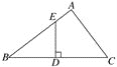
查看答案和解析>>【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数图像过点P(0,6),且平行于直线y=-2x
(1)求该一次函数的解析式
(2)若点A(
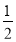 ,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。
,a)、B(2,b)在该函数图像上,试判断a、b的大小关系,并说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘一辆汽车沿公路东西方向检修线路,约定向东为正,某天从A地出发到收工时行走记录为(单位:千米):
+15、—2、+5、—1、—3、—2、+4、—5
(1)计算收工时,检修小组在A地的哪一边,距A地多远?
(2)若每千米汽车耗油量为0.4升,求出发到收工检修小组耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,点D是边AB的中点,CE∥AB,且AB=2CE,连结BE、CD。

(1)求证:四边形BECD是平行四边形;
(2)用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)
相关试题

