【题目】经过建设者三年多艰苦努力地施工,贯通我市A、B两地又一条高速公路全线通车.已知原来A地到B地普通公路长150km,高速公路路程缩短了30km,如果一辆小车从A地到B地走高速公路的平均速度可以提高到原来的1.5倍,需要的时间可以比原来少用1小时.求小车走普通公路的平均速度是多少?
参考答案:
【答案】小车走普通公路的平均速度是70千米/时.
【解析】分析:根据题意设小汽车原来的平均速度为x千米/时,则现在走高速公路的平均速度是1.5x千米/时,根据提速后需要的时间可以比原来少用1小时列方程即可;正确求解方程即可解答,注意分式方程需要检验.
详解:设小车走普通公路的平均速度是x千米/时,得
![]() ,
,
解得x=70 ,
经检验:x=70是原方程的解,且符合题意 .
答:小车走普通公路的平均速度是70千米/时。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,点D是边AB的中点,CE∥AB,且AB=2CE,连结BE、CD。

(1)求证:四边形BECD是平行四边形;
(2)用无刻度的直尺画出△ABC边BC上的中线AG(保留画图痕迹)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有两点A、B,点A表示的数是4,点B表示的数是﹣11,点C是数轴上一动点.
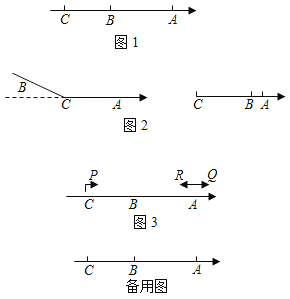
(1)如图1,若点C在点B的左侧,且BC:AB=3:5,求点C到原点的距离.
(2)如图2,若点C在A、B两点之间时,以点C为折点,将此数轴向右对折,当A、B两点之间的距离为1时,求C点在数轴上对应的数是多少?
(3)如图3,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度的2倍少5个单位长度/秒.经过4秒,点P、Q之间的距离是点Q、R之间距离的一半,求动点Q的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于
 的长为半径画弧,两弧交于P,Q两点;
的长为半径画弧,两弧交于P,Q两点; ②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

-
科目: 来源: 题型:
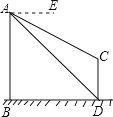
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数
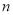 ,在计算
,在计算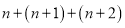 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数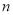 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算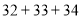 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算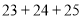 时,个位产生了进位.
时,个位产生了进位.(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
相关试题

