【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题 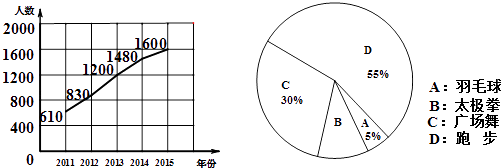
(1)2015年比2011年增加人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数.
参考答案:
【答案】
(1)990
(2)解:1600×55%=880(人);
答:2015年参与跑步项目的人数为880人
(3)解:1600×(1+15%)×(1﹣55%﹣30%﹣5%)=184(人);
答:估计2016年参加太极拳的人数为184人
【解析】解:(1)1600﹣610=(人);
故答案为:990人;
(1)用2015年的人数﹣2011年的人数即可;(2)用2015年总人数×参与跑步项目的人数所占的百分数即可;(3)2015年总人数×(1+15%)×参加太极拳的人数所占的百分数即可.本题考查了折线统计图、扇形统计图、用样本估计总体等知识;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义,我们把对角线互相垂直的四边形叫做垂美四边形.
概念理解:如图②,在四边形ABCD中,如果AB=AD,CB=CD,那么四边形ABCD是垂美四边形吗?请说明理由.
性质探究:如图①,垂美四边形ABCD两组对边AB、CD与BC、AD之间有怎样的数量关系?写出你的猜想,并给出证明.
问题解决:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE.若AC=2,AB=5,则①求证:△AGB≌△ACE;
②GE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为
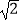 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
的等腰直角三角形DEF的费马点,则PD+PE+PF= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.

(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的两个顶点A、C在反比例函数y=
 (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
相关试题

