【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.
参考答案:
【答案】
(1)解:∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
∴3= ![]() ,点C与点A关于原点O对称,
,点C与点A关于原点O对称,
∴k=6,C(﹣2,﹣3),
即k的值是6,C点的坐标是(﹣2,﹣3)
(2)解:∵△APO的面积为2,点A的坐标是(2,3),
∴ ![]() ,得OP=2,
,得OP=2,
设过点P(0,2),点A(2,3)的直线解析式为y=ax+b,
![]()
解得, ![]() ,
,
即直线PC的解析式为y= ![]() ,
,
将y=0代入y= ![]() ,得x═﹣4,
,得x═﹣4,
∴OP=4,
∵A(2,3),C(﹣2,﹣3),
∴AC= ![]() ,
,
设点D到AC的距离为m,
∵S△ACD=S△ODA+S△ODC,
∴ ![]() ,
,
解得,m= ![]() ,
,
即点D到直线AC的距离是 ![]()
【解析】(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.本题考查反比例函数与一次函数的交点问题、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据等积法可以求得点D到直线AC的距离.本题考查反比例函数与一次函数的交点问题、平行四边形的性质,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题
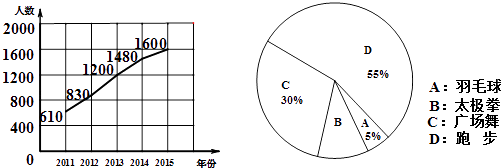
(1)2015年比2011年增加人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.

(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形

(1)求证:△DFB是等腰三角形;
(2)若DA= AF,求证:CF⊥AB.
AF,求证:CF⊥AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)
(1)当k= 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根;
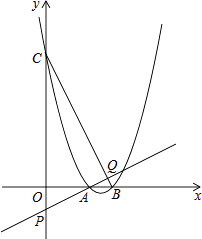
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证: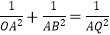 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC与BD交于点O,若增加一个条件,使ABCD成为菱形,下列给出的条件不正确的是( )

A.AB=AD
B.AC⊥BD
C.AC=BD
D.∠BAC=∠DAC
相关试题

