【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射,若被
反射,若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且
平行,且![]() ,则
,则![]() _________,
_________,![]() ________.
________.
(2)在(1)中,若![]() ,则
,则![]() _______;若
_______;若![]() ,则
,则![]() ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜![]() 、
、![]() 的夹角
的夹角![]() ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请说明理由.
平行.请说明理由.

参考答案:
【答案】(1)100°,90°;(2)90°,90°;(3)90°,理由见解析.
【解析】
试题根据入射角与反射角相等,可得∠1=∠4,∠5=∠6.
(1)根据邻补角的定义可得∠7=80°,根据m∥n,所以∠2=100°,∠5=40°,根据三角形内角和为180°,即可求出答案;
(2)结合题(1)可得∠3的度数都是90°;
(3)证明m∥n,由∠3=90°,证得∠2与∠7互补即可.
试题解析: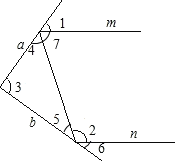
(1) ![]()
∵入射角与反射角相等,即∠1=∠4,∠5=∠6,
根据邻补角的定义可得![]()
根据m∥n,所以![]()
所以![]()
根据三角形内角和为![]() 所以
所以![]()
(2) ![]()
由(1)可得∠3的度数都是![]()
(3) ![]()
理由:因为∠3=![]()
所以∠4+∠5=![]()
又由题意知∠1=∠4,∠5=∠6,
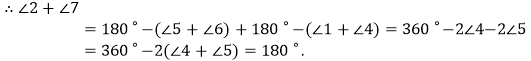 由同旁内角互补,两直线平行,可知:m∥n.
由同旁内角互补,两直线平行,可知:m∥n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠BAP与∠APD互补,∠1=∠2,试说明:∠E=∠F.请在下面的括号中填上理由.

解:∵∠BAP与∠APD互补( ),
∴AB∥CD( ),
∴∠BAP=∠APC( ).
又∵∠1=∠2( ),
∴∠BAP-∠1=∠APC-∠2( ),
即∠3=∠4,
∴AE∥PF( ),
∴∠E=∠F( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和CD相交于点O,∠COE=90°,OD平分∠BOF,∠BOE=50°.
(1)求∠AOC的度数;
(2)求∠EOF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

-
科目: 来源: 题型:
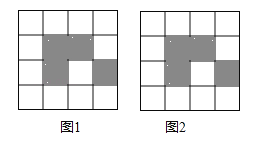
查看答案和解析>>【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
相关试题

