【题目】如图,在Rt△ABC中,∠ACB=90°,点D,E分别在AB,AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CF,连接EF.
(1)补充完成图形;
(2)若EF∥CD,求证:∠BDC=90°.

参考答案:
【答案】见解析
【解析】试题分析:(1)根据题意补全图形,如图所示;
(2)由旋转的性质得到![]() 为直角,由EF与CD平行,得到
为直角,由EF与CD平行,得到![]() 为直角,利用SAS得到
为直角,利用SAS得到![]() 与
与![]() 全等,利用全等三角形对应角相等即可得证.
全等,利用全等三角形对应角相等即可得证.
试题解析:(1)补全图形,如图所示;

(2)由旋转的性质得: ![]()
∴∠DCE+∠ECF=![]() ,
,
∵∠ACB=![]() ,
,
∴∠DCE+∠BCD=![]() ,
,
∴∠ECF=∠BCD,
∵EF∥DC,
∴∠EFC+∠DCF=![]() ,
,
∴∠EFC=![]() ,
,
在△BDC和△EFC中,
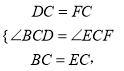
∴△BDC≌△EFC(SAS),
∴∠BDC=∠EFC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列结论错误的是( ).

A.AE∥BC B. ∠ADE=∠BDC
C.△BDE是等边三角形 D. △ADE的周长是9
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线
 射到平面镜
射到平面镜 上,被
上,被 反射到平面镜
反射到平面镜 上,又被
上,又被 反射,若被
反射,若被 反射出的光线
反射出的光线 与光线
与光线 平行,且
平行,且 ,则
,则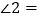 _________,
_________, ________.
________.(2)在(1)中,若
 ,则
,则 _______;若
_______;若 ,则
,则 ________;
________;(3)由(1)、(2),请你猜想:当两平面镜
 、
、 的夹角
的夹角 ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜 上的光线
上的光线 ,经过平面镜
,经过平面镜 、
、 的两次反射后,入射光线
的两次反射后,入射光线 与反射光线
与反射光线 平行.请说明理由.
平行.请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上.将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.

(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过的区域的面积.
-
科目: 来源: 题型:
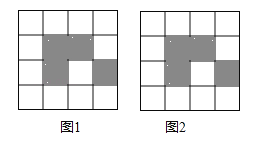
查看答案和解析>>【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
-
科目: 来源: 题型:
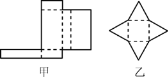
查看答案和解析>>【题目】观察图,回答下列问题:
(1)甲、乙两图分别能折成什么几何体?简述它们的特征;
(2)设几何体的面数为F,顶点数为V,棱数为E,请计算(1)中两个几何体的F+V-E的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,它表示甲乙两人从同一个地点出发后的情况.根据图像判断,下列说法错误的是()

A. 甲是 8 点出发的
B. 乙是 9 点出发的,到 10 点时,他大约走了 10 千米
C. 到 10 点为止,乙的速度快
D. 两人在 12 点再次相遇
相关试题

