【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款![]() 万元,乙工程队工程款
万元,乙工程队工程款![]() 万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用
万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用![]() 天;③若甲乙两队合作
天;③若甲乙两队合作![]() 天,余下的工程由乙队单独也正好如期完成.
天,余下的工程由乙队单独也正好如期完成.
(1)甲、乙单独完成各需要多少天?
(2)在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
参考答案:
【答案】(1)甲单独20天,乙单独25天完成.(2)方案③最节省.
【解析】
(1)设这项工程的工期是x天,根据甲队单独完成这项工程刚好如期完成,乙队单独完成这项工程要比规定日期多用5天,若甲、乙两队合做4天,余下的工程由乙队单独做也正好如期完成以及工作量=工作时间×工作效率可列方程求解.
(2)根据题意可得方案①、③不耽误工期,符合要求,再求出各自的费用,方案②显然不符合要求.
(1)设规定日期x天完成,则有:![]()
解得x=20.
经检验得出x=20是原方程的解;
答:甲单独20天,乙单独25天完成.
(2)方案①:20×1.5=30(万元),
方案②:25×1.1=27.5(万元 ),但是耽误工期,
方案③:4×1.5+1.1×20=28(万元).
所以在不耽误工期的前提下,选第三种施工方案最节省工程款.
所以方案③最节省.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):

根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在生活人们已经离不开密码,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式
 ,因式分解的结果是
,因式分解的结果是 ,若取
,若取 ,
, 时则各个因式的值是:
时则各个因式的值是: ,
, ,
, ,把这些值从小到大排列得到
,把这些值从小到大排列得到 ,于是就可以把“018162”作为一个六位数的密码.对于多项式
,于是就可以把“018162”作为一个六位数的密码.对于多项式 ,取
,取 ,
, 时,请你写出用上述方法产生的密码_________.
时,请你写出用上述方法产生的密码_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.
(1)求购买甲、乙两种树苗各多少棵?
(2)为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个大小不同的等腰直角三角板按图①所示的位置放置,图②是由它抽象画出的几何图形,
 ,
, ,
, ,
, ,
, ,
, 在同一条直线上,连接
在同一条直线上,连接 .
.(1)请找出图②中与
 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)求证:
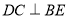 .
.
-
科目: 来源: 题型:
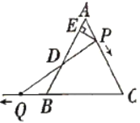
查看答案和解析>>【题目】如图,
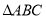 是边长为
是边长为 的等边三角形,
的等边三角形, 是
是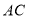 边上一动点,由
边上一动点,由 向
向 运动(与
运动(与 、
、 不重合),
不重合),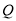 是
是 延长线上一动点,与点
延长线上一动点,与点 同时以相同的速度由
同时以相同的速度由 向
向 延长线方向运动(
延长线方向运动(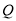 不与
不与 重合),过
重合),过 作
作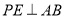 于
于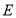 ,连接
,连接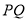 交
交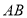 于
于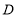 .
.
(1)若
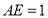 时,求
时,求 的长;
的长;(2)当
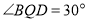 时,求
时,求 的长;
的长;(3)在运动过程中线段
 的长是否发生变化?如果不变,求出线段
的长是否发生变化?如果不变,求出线段 的长;如果发生变化,请说明理由.
的长;如果发生变化,请说明理由.
相关试题

