【题目】在四边形中![]() ,点
,点![]() 为
为![]() 边上的一点,点
边上的一点,点![]() 为对角线
为对角线![]() 上的一点,且
上的一点,且![]() .
.
(1)若四边形![]() 为正方形.
为正方形.
①如图1,请直接写出![]() 与
与![]() 的数量关系___________;
的数量关系___________;
②将![]() 绕点
绕点![]() 逆时针旋转到图2所示的位置,连接
逆时针旋转到图2所示的位置,连接![]() ,猜想
,猜想![]() 与
与![]() 的数量关系并说明理由;
的数量关系并说明理由;
(2)如图3,若四边形![]() 为矩形,
为矩形,![]() ,其它条件都不变,将
,其它条件都不变,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() ,请在图3中画出草图,并直接写出
,请在图3中画出草图,并直接写出![]() 与
与![]() 的数量关系.
的数量关系.

参考答案:
【答案】(1)①DF=![]() AE,②DF=
AE,②DF=![]() AE,理由见解析;(2)DF′=
AE,理由见解析;(2)DF′=![]() AE′.
AE′.
【解析】
试题分析:(1)①利用正方形的性质得△ABD为等腰直角三角形,则BF=![]() AB,再证明△BEF为等腰直角三角形得到BF=
AB,再证明△BEF为等腰直角三角形得到BF=![]() BE,所以BD﹣BF=
BE,所以BD﹣BF=![]() AB﹣
AB﹣![]() BE,从而得到DF=
BE,从而得到DF=![]() AE;
AE;
②利用旋转的性质得∠ABE=∠DBF,加上![]() =
=![]() ,则根据相似三角形的判定可得到△ABE∽△DBF,所以
,则根据相似三角形的判定可得到△ABE∽△DBF,所以![]() =
=![]() ;
;
(2)先画出图形得到图3,利用勾股定理得到BD=![]() AB,再证明△BEF∽△BAD得到
AB,再证明△BEF∽△BAD得到![]() ,则
,则![]() =
=![]() ,接着利用旋转的性质得∠ABE′=∠DBF′,BE′=BE,BF′=BF,所以
,接着利用旋转的性质得∠ABE′=∠DBF′,BE′=BE,BF′=BF,所以![]() =
=![]() ,然后根据相似三角形的判定方法得到△ABE′∽△DBF′,再利用相似的性质可得
,然后根据相似三角形的判定方法得到△ABE′∽△DBF′,再利用相似的性质可得![]() =
=![]() .
.
试题解析:(1)①∵四边形ABCD为正方形,∴△ABD为等腰直角三角形,
∴BF=![]() AB,
AB,
∵EF⊥AB,∴△BEF为等腰直角三角形,BF=![]() BE,
BE,
∴BD﹣BF=![]() AB﹣
AB﹣![]() BE,即DF=
BE,即DF=![]() AE;
AE;
故答案为DF=![]() AE;
AE;
②DF=![]() AE.理由如下:
AE.理由如下:
∵△EBF绕点B逆时针旋转到图2所示的位置,∴∠ABE=∠DBF,
∵![]() =
=![]() ,
,![]() =
=![]() ,∴
,∴![]() ,
,
∴△ABE∽△DBF,∴![]() =
=![]() ,
,
即DF=![]() AE;
AE;
(2)如图3,∵四边形ABCD为矩形,
∴AD=BC=mAB,∴BD=![]() =
=![]() AB,
AB,
∵EF⊥AB,∴EF∥AD,∴△BEF∽△BAD,
∴![]() ,∴
,∴![]() =
=![]() ,
,
∵△EBF绕点B顺时针旋转α(0°<α<90°)得到△E'BF',
∴∠ABE′=∠DBF′,BE′=BE,BF′=BF,
∴![]() =
=![]() ,
,
∴△ABE′∽△DBF′,
∴![]() =
=![]() ,
,
即DF′=![]() AE′.
AE′.

-
科目: 来源: 题型:
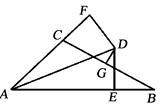
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DE , DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG , 其中不正确的结论的个数为( )

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是真命题的是( )
A.同位角相等B.相等的角是对顶角
C.邻补角一定互补D.有且只有一条直线与已知直线垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D , DE⊥AB , DF⊥AC , 垂足分别为E , F , AB=11,AC=5,则BE= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=3,y=1是方程3x﹣ay=2的一个解,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC和△ADE都是等边三角形.
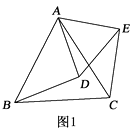
(1)求证:BD=CE;
(2)如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.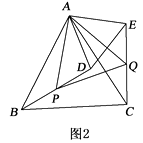
相关试题

