【题目】如图1,△ABC和△ADE都是等边三角形.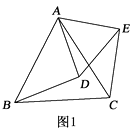
(1)求证:BD=CE;
(2)如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.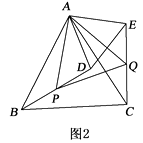
参考答案:
【答案】
(1)证明:∵ △ABC和△ADE都是等边三角形,
∴AB=AC,AD=AE,∠BAC =∠DAE=60°.
∴∠BAC-∠DAC =∠DAE-∠DAC,即∠BAD =∠CAE.
在△ABD与△ACE中 , 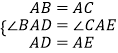
∴△ABD≌△ACE(SAS)
∴BD=CE
(2)解:△APQ是等边三角形,理由如下
∵P是BD中点,Q是CE中点,BD=CE,∴BP=CQ .
∵△ABD≌△ACE ∴∠ABP=∠ACQ .
在△ABP与△ACQ中 ∵ 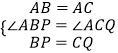 ∴△ABP≌△ACQ(SAS),
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ ,
∴∠BAP+∠CAP =∠CAQ+∠CAP,
∴∠PAQ=∠BAC=60°
∴△APQ是等边三角形
【解析】第1小题,根据两个等边三角形得到AB=AC,AD=AE,∠BAC =∠DAE=60°,然后用边角边可证明△ABD≌△ACE,问题得证;第2小题,由第1问的结论和第2问的已知条件可证△ABP≌△ACQ,得到AP=AQ,∠BAP=∠CAQ,从而可得∠PAQ=∠BAC=60°,于是问题可得证。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形中
 ,点
,点 为
为 边上的一点,点
边上的一点,点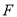 为对角线
为对角线 上的一点,且
上的一点,且 .
.(1)若四边形
 为正方形.
为正方形.①如图1,请直接写出
 与
与 的数量关系___________;
的数量关系___________;②将
 绕点
绕点 逆时针旋转到图2所示的位置,连接
逆时针旋转到图2所示的位置,连接 ,猜想
,猜想 与
与 的数量关系并说明理由;
的数量关系并说明理由;(2)如图3,若四边形
 为矩形,
为矩形, ,其它条件都不变,将
,其它条件都不变,将 绕点
绕点 顺时针旋转
顺时针旋转 得到
得到 ,连接
,连接 ,请在图3中画出草图,并直接写出
,请在图3中画出草图,并直接写出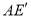 与
与 的数量关系.
的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=3,y=1是方程3x﹣ay=2的一个解,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某课外小组的同学们实践活动中调查了20户家庭某月用电量,如表所示:
用电量(度)
120
140
160
180
220
户数
2
4
5
7
2
则这户家庭用电量的众数和中位数分别是( )
A.180,160
B.160,180
C.160,160
D.180,180 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点A(4,0),点B是y轴正半轴上一点,如图1,以AB为直角边作等腰直角三角形ABC.

(1)当点B坐标为(0,1)时,求点C的坐标;
(2)如图2,以OB为直角边作等腰直角△OBD , 点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有四张背面完全相同的纸牌
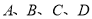 ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.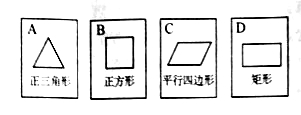
(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用
 表示).
表示).
相关试题

