Question

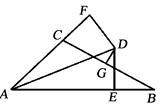
【题目】如图，AD是△ABC的角平分线，DE ， DF分别是△ABD和△ACD的高，连接EF交AD于G.下列结论：①AD垂直平分EF；②EF垂直平分AD；③AD平分∠EDF；④当∠BAC为60°时，AG=3DG ， 其中不正确的结论的个数为（ ）

A.1
B.2
C.3
D.4

Answer 1

【答案】A
【解析】根据角平分线的性质定理可得DE=DF，利用HL定理可证得Rt△ADE≌Rt△ADF，即可得∠ADE=∠ADF ，所以AD平分∠EDF，③正确； 根据等腰三角形的三线合一可得AD垂直平分EF，①正确，②错误；由∠BAC=60°可得∠EAD=30°，根据在直角三角形中，30°的锐角所对的直角边是斜边的一半可得2DG=DE，2DE=AD，所以AD=4DG，即可得AG=3DG，所以④正确，故答案为：A.

根据角平分线的性质定理可判断选项③的正误，根据等腰三角形的三线合一可判断①②的正误根据在直角三角形中，30°的锐角所对的直角边是斜边的一半可判断④的正误。