搜索
【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，﹣1）、B（﹣1，1）、C（0，﹣2）．
（1）点B关于坐标原点O对称的点的坐标为；
（2）将△ABC绕点C顺时针旋转90°，画出旋转后得到的△A1B1C；
（3）求过点B1的反比例函数的解析式．
参考答案：
【答案】
（1）（1，﹣1）
（2）
解：所画图形如下：
（3）
解：由（2）得B1点坐标为（3，﹣1），
设过点B1的反比例函数解析式为 
，
把点B1 （3，﹣1）代入 中，得k=﹣3．
故可得反比例函数解析式为 
【解析】解：（1）点B关于坐标原点O对称的点的坐标为（1，﹣1）；
（1）根据两个点关于原点对称时，它们的坐标符号相反，可得出答案；（2）分别找到各点的对应点，然后顺次连接即可得出旋转后得到的△A1B1C．（3）根据（2）所得的图形，可得出点B1的坐标，然后利用待定系数发可求出过点B1的反比例函数的解析式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线
，直线
和直线
交于点C、D,直线上有一点P.(1)如图1，点P在C、D之间运动时，∠PAC、∠APB、∠PBD之间有什么关系？并说明理由。
(2)若点P在C、D两点外侧运动时(P点与C、D不重合，如图2、3),试直接写出∠PAC、∠APB、∠PBD之间有什么关系，不必写理由。
图1 图2 图3
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学为打造书香校园，计划购进甲、乙两种规格的书柜放置新购进的图书，调查发现，若购买甲种书柜3个、乙种书柜2个，共需资金1020元；若购买甲种书柜4个，乙种书柜3个，共需资金1440元．
（1）甲、乙两种书柜每个的价格分别是多少元？
（2）若该校计划购进这两种规格的书柜共20个，其中乙种书柜的数量不少于甲种书柜的数量，学校至多能够提供资金4320元，请设计几种购买方案供这个学校选择．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线
分别交x轴、y轴于A、B两点，线段AB的垂直平分线分别交x轴、y轴于C、D两点．
（1）求点C的坐标；
（2）求△BCD的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】列方程或方程组解应用题:
为了响应学校提出的“节能减排，低碳生活”的倡议，班会课上小李建议每位同学都践行“双面打印，节约用纸”．他举了一个实际例子：打印一份资料，如果用A4厚型纸单面打印，总质量为400克，将其全部改成双面打印，用纸将减少一半；如果用A4薄型纸双面打印，总质量为160克.已知每页薄型纸比厚型纸轻0.8克，求例子中的A4厚型纸每页的质量.（墨的质量忽略不计）
-
科目： 来源： 题型：
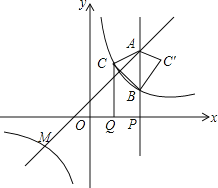
查看答案和解析>>【题目】如图，点M（－3，m）是函数y＝x＋1与反比例函数
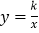（k≠0）的图象的一个交点．（1）求反比例函数表达式；
（2）点P是x轴正半轴上的一个动点，设OP＝a（a≠2），过点P作垂直于x轴的直线，分别交一次函数，反比例函数的图象于点A，B，过OP的中点Q作x轴的垂线，交反比例函数的图象于点C，△ABC′与△ABC关于直线AB对称．
①当a＝4时，求△ABC′的面积；
②若△AMC与△AMC′的面积相等，求a的值 ．
-
科目： 来源： 题型：
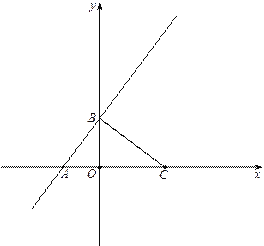
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点C的坐标为（4，0），一次函数
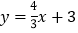的图像分别交x轴、y轴于点A、点B.⑴ 若点D是直线AB在第一象限内的点，且BD＝BC，试求出点D的坐标.
⑵ 在⑴的条件下，若点Q是坐标轴上的一个动点，试探索在第一象限是否存在另一个点P，使得以B、D、P、Q为顶点的四边形是菱形（BD为菱形的一边）？若存在，请直接写出点P的坐标；若不存在，请说明理由．
相关试题
