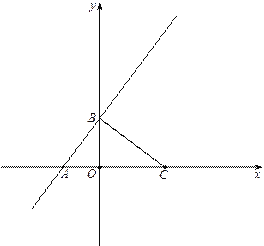
【题目】如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数![]() 的图像分别交x轴、y轴于点A、点B.
的图像分别交x轴、y轴于点A、点B.
⑴ 若点D是直线AB在第一象限内的点,且BD=BC,试求出点D的坐标.
⑵ 在⑴的条件下,若点Q是坐标轴上的一个动点,试探索在第一象限是否存在另一个点P,使得以B、D、P、Q为顶点的四边形是菱形(BD为菱形的一边)?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)点D 的坐标为(3,7)
(2)点P的坐标为(3,12)或(3,2)或(7,4)
【解析】试题分析:(1)先求出OB=3,进而求出BC=5,再用勾股定理建立方程求出点D;
(2)分点Q在y轴和x轴,两种情况讨论,先利用菱形的性质求出BQ=5进而得出点Q的坐标,再利用菱形的对边平行即可求出点P的坐标.
试题解析:(1)如图1,设点D(3a,4a+3),
过点D作DE⊥y轴于E,把x=0代入y=![]() x+3中,得,y=3,
x+3中,得,y=3,
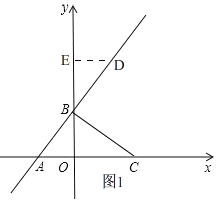
∴OB=3,
∴BE=OE-OB=4a+3-3=4a,BC=![]() =5,
=5,
在Rt△BED中,根据勾股定理得,(3a)2+(4a)2=52,
∴a=±1,
∵点D在第一象限,
∴a=1,
∴D(3,7);
(2)由(1)知,BD=BC=5,
①当点Q在y轴上时,
设Q(0,q),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴PQ∥BD,DP∥BQ,
∴点P的横坐标为3,
∵四边形BDPQ是菱形,
∴BQ=BD=5,
∵B(0,3),
∴Q(0,8)或(0,-2),
Ⅰ、当点Q(0,8)时,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴直线PQ的解析式为y=![]() x+8,
x+8,
当x=3时,y=12,
∴P(3,12),
Ⅱ、点Q(0,-2)时,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴直线PQ的解析式为y=![]() x-2,
x-2,
当x=3时,y=2,
∴P(3,2),
②当点Q在x轴上时,
设Q(m,0),),
∵使得以B,D,P,Q为顶点的四边形是菱形(BD为菱形的一边),且点P在第一象限内,
即:四边形BDPQ是菱形,
∴BQ=BD=5,
∵OB=3,
∴OQ=4,
∴Q(-4,0)或(4,0)
Ⅰ、当Q(-4,0)时,∵一次函数y=![]() x+3的图象交x轴于点A,
x+3的图象交x轴于点A,
∴A(-![]() ,0),
,0),
∴点Q在点A的左侧,
∴点P在第二象限内,不符合题意,舍去,
Ⅱ、当点Q(4,0)时,∵四边形BDPQ是菱形,
∴BQ∥DP,PQ∥BD,
∵直线BD的解析式为y=![]() x+3,
x+3,
∴设直线PQ的解析式为y=![]() x+b,
x+b,
∴![]() ×4+b=0,
×4+b=0,
∴b=-![]() ,
,
∴直线PQ的解析式为y=![]() x-
x-![]() ①,
①,
∵B(0,3),Q(4,0),
∴直线BQ的解析式为y=-![]() x+3,
x+3,
∵D(3,7),
∴直线DP的解析式为y=-![]() x+
x+![]() ②,
②,
联立①②解得,x=7,y=4,
∴P(7,4),
即:满足条件的点P的坐标为(3,12)、(3,2)、(7,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)、B(﹣1,1)、C(0,﹣2).

(1)点B关于坐标原点O对称的点的坐标为;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的反比例函数的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程或方程组解应用题:
为了响应学校提出的“节能减排,低碳生活”的倡议,班会课上小李建议每位同学都践行“双面打印,节约用纸”.他举了一个实际例子:打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,总质量为160克.已知每页薄型纸比厚型纸轻0.8克,求例子中的A4厚型纸每页的质量.(墨的质量忽略不计)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M(-3,m)是函数y=x+1与反比例函数
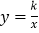 (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点.(1)求反比例函数表达式;
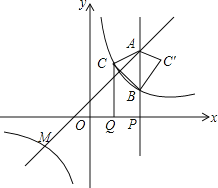
(2)点P是x轴正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
①当a=4时,求△ABC′的面积;
②若△AMC与△AMC′的面积相等,求a的值 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,直线
 ,
, ,
, 分别通过A,B,C三点,且
分别通过A,B,C三点,且 ,若
,若 与
与 的距离为5,
的距离为5, 与
与 的距离为7,则正方形ABCD的面积等于( )
的距离为7,则正方形ABCD的面积等于( )
A. 148 B. 70 C. 144 D. 74
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )

A.100米 B.99米 C.98米 D.74米
-
科目: 来源: 题型:
查看答案和解析>>【题目】2012年4月23日是第17个世界读书日,《教育导报》记者就四川省农村中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本).其中A:1≤x≤3; B:4≤x≤6; C:7≤x≤9;D:x≥10.请你根据两幅图提供的信息解答下列问题:

(1)本次共调查了多少名教师?
(2)补全条形统计图;
(3)计算扇形统计图中扇形D的圆心角的度数.
相关试题

