【题目】如图,已知直线![]() ,直线
,直线![]() 和直线
和直线![]() 交于点C、D,直线
交于点C、D,直线![]() 上有一点P.
上有一点P.
(1)如图1,点P在C、D之间运动时,∠PAC、∠APB、∠PBD之间有什么关系?并说明理由。
(2)若点P在C、D两点外侧运动时(P点与C、D不重合,如图2、3),试直接写出∠PAC、∠APB、∠PBD之间有什么关系,不必写理由。

图1 图2 图3
参考答案:
【答案】(1)详见解析;(2)当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB;当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
【解析】
(1)过点P作PE∥l1,根据两直线平行,内错角相等即可得证;
(2)同理(1)即可得证.
(1)如图,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD;
理由如下: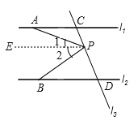
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
(2)如图2,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB;
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB;
如图3,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB;
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).

(1)在如图所示的平面直角坐标系画出该四边形;
(2)四边形ABCD的面积是________;
(3)四边形ABCD内(边界点除外)一共有_____个整点(即横坐标和纵坐标都是整数的点).
-
科目: 来源: 题型:
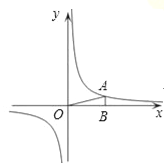
查看答案和解析>>【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=
 (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为 .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=
 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;(3)过原点O的直线l与反比例函数y=
 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(
 )求本次被调查的学生人数.
)求本次被调查的学生人数.(
 )将条形统计图补充完整.
)将条形统计图补充完整.(
 )若该校共有
)若该校共有 名学生,请估计全校选择体育类的学生人数.
名学生,请估计全校选择体育类的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴、y轴于C、D两点.
分别交x轴、y轴于A、B两点,线段AB的垂直平分线分别交x轴、y轴于C、D两点.
(1)求点C的坐标;
(2)求△BCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,﹣1)、B(﹣1,1)、C(0,﹣2).

(1)点B关于坐标原点O对称的点的坐标为;
(2)将△ABC绕点C顺时针旋转90°,画出旋转后得到的△A1B1C;
(3)求过点B1的反比例函数的解析式.
相关试题

