【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)将△ABC向右移平2个单位长度,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
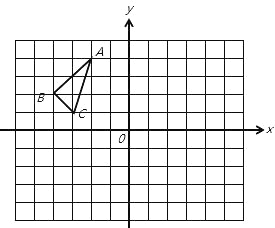
(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)求出三角形ABC的面积
参考答案:
【答案】(1)A1(0,4),B1(-2,2),C1(-1,1)(2)A2(0,-4),B2(2,-2),C2(1,-1)(3)2
【解析】试题分析:
(1)先在坐标系描出平移后的A1、B1、C1,顺次连接这三点即可得到所求△A1B1C1,再写出A1、B1、C1三点的坐标即可;
(2)设点(-1,0)为点D,连接AD并延长至A2,使DA2=DA即可得到A2点,同法作出B2、C2,顺次连接三点即可得到△A2B2C2,再写出三点的坐标即可;
(3)如图2,由S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF即可求出△ABC的面积.
试题解析:
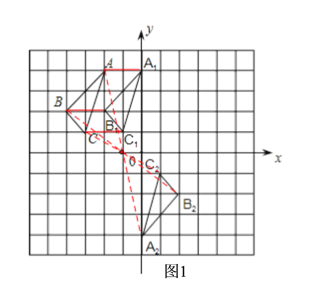
(1)如图1,图中△A1B1C1为所求三角形;三点的坐标分别为:A1(0,4),B1(-2,2),C1(-1,1);
(2)如图1,图中△A2B2C2为所求三角形;三点的坐标分别为:A2(0,-4),B2(2,-2),C2(1,-1);
(3)如图2,S△ABC=S矩形ADEF-S△ADB-S△BEC-S△ACF=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论;
(2)△ABC满足什么条件时四边形ADCF为正方形,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形纸片ABC中,∠B=2∠C,把三角形纸片沿直线AD折叠,点B落在AC边上的E处,那么下列等式成立的是( )

A.AC=AD+BDB.AC=AB+BDC.AC=AD+CDD.AC=AB+CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.

(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是____________,位置关系是____________;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将平行四边形 ABCD 沿对角线 BD 折叠,使点 A 落在A′处,若∠1=∠2=50°,则∠A′的度数为( )

A.100°B.105°C.110°D.115°
-
科目: 来源: 题型:
查看答案和解析>>【题目】对两实数
 ,
, 定义一种新运算,规定
定义一种新运算,规定 .
.例如:
 .
.(1)填空:
 ________;
________; ________.
________.(2)若
 ,求
,求 的值.
的值.(3)若
 ,
, 为整数,且
为整数,且 ,求满足条件的所有
,求满足条件的所有 ,
, 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在长方形
 中,
中,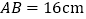 ,
,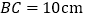 ,动点
,动点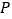 从
从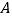 出发,匀速沿
出发,匀速沿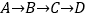 运动,到点
运动,到点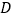 停止;同时动点
停止;同时动点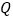 从
从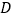 出发,匀速沿
出发,匀速沿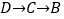 运动,速度是动点
运动,速度是动点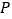 速度的一半,当其中一个点到达终点时,另一个点停止运动.如图②是点
速度的一半,当其中一个点到达终点时,另一个点停止运动.如图②是点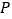 出发后
出发后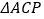 的面积
的面积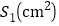 与运动时间
与运动时间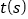 之间的关系图象.
之间的关系图象.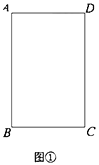
(1)图②中,求
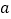 ,
,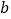 的值.
的值.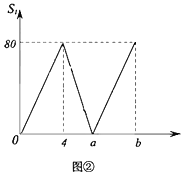
(2)当
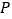 运动多少秒后,
运动多少秒后,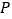 ,
,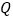 两点相遇.
两点相遇.(3)在点
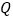 从点
从点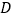 运动到点
运动到点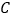 的过程中,记点
的过程中,记点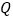 出发后
出发后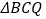 的面积为
的面积为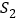 ,当
,当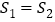 ,时,求动点
,时,求动点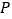 运动的时间
运动的时间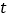 .
.
相关试题

