【题目】某经销商经销的学生用品,他以每件280元的价格购进某种型号的学习机,以每件360元的售价销售时,每月可售出60个,为了扩大销售,该经销商采取降价的方式促销,在销售中发现,如果每个学习机降价1元,那么每月就可以多售出5个.
![]() 降价前销售这种学习机每月的利润是多少元?
降价前销售这种学习机每月的利润是多少元?
![]() 经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
![]() 在
在![]() 的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
参考答案:
【答案】(1)4800元;(2)降价60元;(3)应涨26元每月销售这种学习机的利润能达到10580元.
【解析】
![]() 根据总利润=单个利润×数量列出算式,计算即可求出值;
根据总利润=单个利润×数量列出算式,计算即可求出值;
![]() 设每个学习机应降价x元,根据题意列出方程,求出方程的解即可得到结果;
设每个学习机应降价x元,根据题意列出方程,求出方程的解即可得到结果;
![]() 设应涨y元每月销售这种学习机的利润能达到10580元,根据题意列出方程,求出方程的解即可得到结果.
设应涨y元每月销售这种学习机的利润能达到10580元,根据题意列出方程,求出方程的解即可得到结果.
解:![]() 由题意得:
由题意得:![]() 元
元![]() ,
,
则降价前商场每月销售学习机的利润是4800元;
![]() 设每个学习机应降价x元,
设每个学习机应降价x元,
由题意得:![]() ,
,
解得:![]() 或
或![]() ,
,
由题意尽可能让利于顾客,![]() 舍去,即
舍去,即![]() ,
,
则每个学习机应降价60元;
![]() 设应涨y元每月销售这种学习机的利润能达到10580元,
设应涨y元每月销售这种学习机的利润能达到10580元,
根据题意得:![]() ,
,
方程整理得:![]() ,
,
解得:![]() ,
,
则应涨26元每月销售这种学习机的利润能达到10580元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,
中,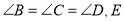 是
是 边上一点,
边上一点, 点
点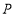 从
从 出发以
出发以 秒的速度沿线段
秒的速度沿线段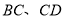 运动,同时点
运动,同时点 从
从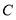 出发,沿线段
出发,沿线段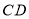 、射线
、射线 运动,当
运动,当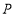 运动到
运动到 ,两点都停止运动.设运动时间为
,两点都停止运动.设运动时间为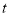 (秒):
(秒):
(1)当
 与
与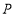 的速度相同,且
的速度相同,且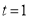 时,求证:
时,求证:
(2)当
 与
与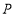 的速度不同,且
的速度不同,且 分别在
分别在 上运动时(如图1),若
上运动时(如图1),若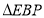 与
与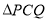 全等,求此时
全等,求此时 的速度和
的速度和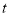 值;
值;(3)当
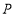 运动到
运动到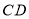 上,
上, 运动到射线
运动到射线 上(如图2),若
上(如图2),若 的速度为
的速度为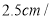 秒,是否存在恰当的边
秒,是否存在恰当的边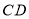 的长,使在运动过程中某一时刻刚好
的长,使在运动过程中某一时刻刚好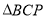 与
与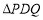 全等,若存在,请求出此时
全等,若存在,请求出此时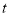 的值和边
的值和边 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校某次外出社会实践活动分为三类,因资源有限,七年级7班分配到20个名额,其中甲类2个、乙类8个、丙类10个,已知该班有50名学生,班主任准备了50个签,其中甲类、乙类、丙类按名额设置、30个空签.采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是多少?
(2)该班小丽同学能有幸去参加实践活动的概率是多少?
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到20%,则还要争取甲类名额多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△AFD和△CEB中,点A、E、F、C在同一条直线上.有下面四个论断:
(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC.
请用其中三个作为条件,余下一个作为结论,进行证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
 是等边三角形,
是等边三角形, 是直线
是直线 上一点,以
上一点,以 为顶点做
为顶点做 .
.  交过
交过 且平行于
且平行于 的直线于
的直线于 ,求证:
,求证: ;当
;当 为
为 的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取
的中点时,(如图1)小明同学很快就证明了结论:他的做法是:取 的中点
的中点 ,连结
,连结 ,然后证明
,然后证明 . 从而得到
. 从而得到 ,我们继续来研究:
,我们继续来研究: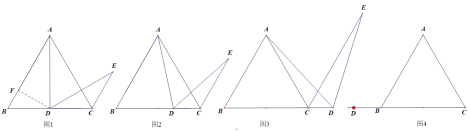
(1)如图2、当D是BC上的任意一点时,求证:

(2)如图3、当D在BC的延长线上时,求证:

(3)当
 在
在 的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明).
的延长线上时,请利用图4画出图形,并说明上面的结论是否成立(不必证明). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.

相关试题

