【题目】在四边形![]() 中,
中,![]() 是
是![]() 边上一点,
边上一点,![]() 点
点![]() 从
从![]() 出发以
出发以![]() 秒的速度沿线段
秒的速度沿线段![]() 运动,同时点
运动,同时点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 、射线
、射线![]() 运动,当
运动,当![]() 运动到
运动到![]() ,两点都停止运动.设运动时间为
,两点都停止运动.设运动时间为![]() (秒):
(秒):

(1)当![]() 与
与![]() 的速度相同,且
的速度相同,且![]() 时,求证:
时,求证:![]()
(2)当![]() 与
与![]() 的速度不同,且
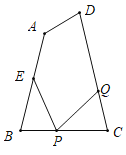
的速度不同,且![]() 分别在
分别在![]() 上运动时(如图1),若
上运动时(如图1),若![]() 与
与![]() 全等,求此时
全等,求此时![]() 的速度和
的速度和![]() 值;
值;
(3)当![]() 运动到
运动到![]() 上,
上,![]() 运动到射线
运动到射线![]() 上(如图2),若
上(如图2),若![]() 的速度为
的速度为![]() 秒,是否存在恰当的边
秒,是否存在恰当的边![]() 的长,使在运动过程中某一时刻刚好
的长,使在运动过程中某一时刻刚好![]() 与
与![]() 全等,若存在,请求出此时
全等,若存在,请求出此时![]() 的值和边
的值和边![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
参考答案:
【答案】(1)见解析;(2)![]() 的速度为3,t的值为2;(3)
的速度为3,t的值为2;(3)![]() 的长为
的长为![]() 时,
时,![]() 两三角形全等
两三角形全等
【解析】
(1)根据SAS即可证明△EBP≌△PCQ.
(2)正确寻找全等三角形的对应边,根据路程,速度,时间的关系即可解决问题.
(3)分两种情形分别构建方程组即可解决问题.
(1)由题意:BP=CQ=1×2=2(cm),
∵BC=8cm,BE=6cm,
∴PC=8-2=6(cm),
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
(2)设![]() 的速度为
的速度为![]() ,
,
则![]() ,
,
分两种情况:
①当![]() 时,
时,![]() ,
,
即![]() ,解得,
,解得,![]() (舍去)
(舍去)
② 当![]() 时,
时,![]() ,
,
即![]() ,解得,
,解得,![]()
Q的速度为3,t的值为2.
(3)设![]() ,则
,则![]() ,
,

分两种情况:
①当![]() 时,
时,![]() ,
,
即![]() ,解得,
,解得,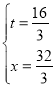
②![]() ,
,![]()
即![]() ,解得
,解得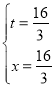
故:当![]() 的长为
的长为![]() 时,
时,![]() 两三角形全等.
两三角形全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,到达目的地后停止,设慢车行驶时间为
 小时,两车之间的距离为
小时,两车之间的距离为 千米,两者的关系如图所示,根据图象探究:
千米,两者的关系如图所示,根据图象探究:
(1)看图填空:两车出发 小时,两车相遇;
(2)求快车和慢车的速度;
(3)求线段
 所表示的
所表示的 与
与 的关系式,并求两车行驶
的关系式,并求两车行驶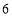 小时两车相距多少千米.
小时两车相距多少千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
①请画出△ABC关于y轴对称的△A1B1C1;
②请画出△ABC关于x轴对称的△A2B2C2的各点坐标;
③在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是关于
是关于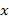 的方程
的方程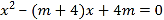 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形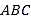 的两条边长,则
的两条边长,则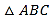 的周长为( )
的周长为( )A. 6 B. 8 C. 10 D. 8或10
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校某次外出社会实践活动分为三类,因资源有限,七年级7班分配到20个名额,其中甲类2个、乙类8个、丙类10个,已知该班有50名学生,班主任准备了50个签,其中甲类、乙类、丙类按名额设置、30个空签.采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是多少?
(2)该班小丽同学能有幸去参加实践活动的概率是多少?
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到20%,则还要争取甲类名额多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某经销商经销的学生用品,他以每件280元的价格购进某种型号的学习机,以每件360元的售价销售时,每月可售出60个,为了扩大销售,该经销商采取降价的方式促销,在销售中发现,如果每个学习机降价1元,那么每月就可以多售出5个.
 降价前销售这种学习机每月的利润是多少元?
降价前销售这种学习机每月的利润是多少元? 经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元?
经销商销售这种学习机每月的利润要达到7200元,且尽可能让利于顾客,求每个学习机应降价多少元? 在
在 的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
的销售中,销量可好,经销商又开始涨价,涨价后每月销售这种学习机的利润能达到10580元吗?若能,请求出涨多少元;若不能,请说明理由.
相关试题

