【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
参考答案:
【答案】(1)k≤![]() ;(2)k=﹣1.
;(2)k=﹣1.
【解析】
(1)根据方程有实数根得出△=[﹣(2k﹣1)]2﹣4×1×(k2+k﹣1)=﹣8k+5≥0,解之可得;
(2)利用根与系数的关系可用k表示出x1+x2和x1x2的值,根据条件可得到关于k的方程,可求得k的值,注意利用根的判别式进行取舍.
(1)∵关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根,
∴△≥0,即[﹣(2k﹣1)]2﹣4×1×(k2+k﹣1)=﹣8k+5≥0,
解得k≤![]() ;
;
(2)由根与系数的关系可得x1+x2=2k﹣1,x1x2=k2+k﹣1,
∴x12+x22=(x1+x2)2﹣2x1x2=(2k﹣1)2﹣2(k2+k﹣1)=2k2﹣6k+3,
∵x12+x22=11,
∴2k2﹣6k+3=11,解得k=4,或k=﹣1,
∵k≤![]() ,
,
∴k=4(舍去),
∴k=﹣1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
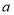 、
、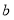 、
、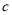 在数轴上的位置如图所示,回答下列问题:
在数轴上的位置如图所示,回答下列问题:
(1)化简:
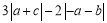 ;
; (2)令
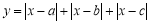 ,请问
,请问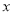 满足什么条件时,
满足什么条件时,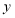 有最小值,并求出该最小值.
有最小值,并求出该最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
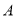 地某厂和
地某厂和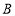 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,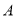 地某厂可支援外地
地某厂可支援外地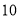 台,
台,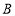 地某厂可支援外地
地某厂可支援外地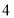 台,现决定给
台,现决定给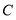 地
地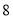 台,
台,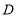 地
地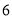 台,已知从
台,已知从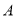 运往
运往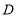 、
、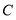 两地的运费分别是
两地的运费分别是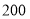 元每台、
元每台、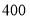 元每台,从
元每台,从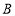 运往
运往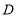 、
、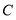 两地的运费分别是
两地的运费分别是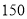 元每台、
元每台、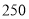 元每台.
元每台.(1)设
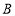 地某厂运往
地某厂运往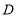 地
地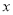 台,求总运费为多少元?
台,求总运费为多少元? (2)在(1)中,当
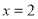 时,总运费是多少元?
时,总运费是多少元? -
科目: 来源: 题型:
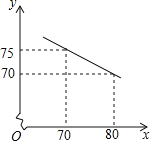
查看答案和解析>>【题目】为早日实现脱贫奔小康的宏伟目标,我市结合本地丰富的山水资源,大力发展旅游业,王家庄在当地政府的支持下,办起了民宿合作社,专门接待游客,合作社共有80间客房.根据合作社提供的房间单价x(元)和游客居住房间数y(间)的信息,乐乐绘制出y与x的函数图象如图所示:
(1)求y与x之间的函数关系式;
(2)合作社规定每个房间价格不低于60元且不超过150元,对于游客所居住的每个房间,合作社每天需支出20元的各种费用,房价定为多少时,合作社每天获利最大?最大利润是多少?
-
科目: 来源: 题型:
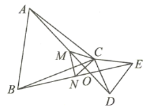
查看答案和解析>>【题目】ΔABC、ΔCDE都是等边三角形,AD、BE相交于点O,点M、点N分别是线段AD、BE的中点.
(1)证明: AD=BE.(2)求∠DOE的角度。(3)证明:ΔMNC是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了
 ,
, 两种型号家用净水器.已知购进2台
两种型号家用净水器.已知购进2台 型号家用净水器比1台
型号家用净水器比1台 型号家用净水器多用200元;购进3台
型号家用净水器多用200元;购进3台 型号净水器和2台
型号净水器和2台 型号家用净水器共用6600元
型号家用净水器共用6600元(1)求
 ,
, 两种型号家用净水器每台进价各为多少元?
两种型号家用净水器每台进价各为多少元?(2)该商家用不超过26400元共购进
 ,
, 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价
两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价 后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进
后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进 ,
, 两种型号家用净水器各多少台?(注:毛利润
两种型号家用净水器各多少台?(注:毛利润 售价
售价 进价)
进价)
相关试题

