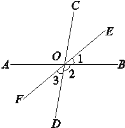
【题目】如图,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
参考答案:
【答案】(1) ∠2=100°, ∠3=40°;(2)平分,理由见解析.
【解析】(1)根据邻补角的定义,即可求得∠2的度数,根据角平分线的定义和平角的定义即可求得∠3的度数;
(2)根据OF分∠AOD的两部分角的度数即可说明.
(1)∵∠BOC+∠2=180°,∠BOC=80°,
∴∠2=180°-80°=100°;
∵OE是∠BOC的角平分线,
∴∠1=40°.
∵∠1+∠2+∠3=180°,
∴∠3=180°-∠1-∠2=180°-40°-100°=40°.
(2)∵∠2+∠3+∠AOF=180°,
∴∠AOF=180°-∠2-∠3=180°-100°-40°=40°.
∴∠AOF=∠3=40°,
∴OF平分∠AOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
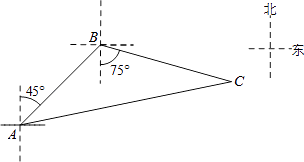
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的进度均保持不变).储运部库存物资w(吨)与时间t(小时)之间的函数关系如图所示,请问这批物资从开始调进到全部调出需要多长时间?

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系
在平面直角坐标系 中的位置如图所示.
中的位置如图所示.(1)作
 关于点
关于点 成中心对称的
成中心对称的 .
.(2)将
 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的 .
.(3)在
 轴上求作一点
轴上求作一点 ,使
,使 的值最小
的值最小 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,OF平分∠AOE,∠1=15°,则下列结论中不正确的是( )
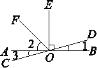
A. ∠2=45° B. ∠1=∠3 C. ∠EOD与∠3互为余角 D. ∠FOD=110°
-
科目: 来源: 题型:
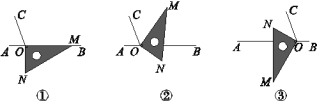
查看答案和解析>>【题目】如图①,O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一三角尺的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角尺绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数;
(2)将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为________(直接写出结果);
(3)将图①中的三角尺绕点O顺时针旋转至图③,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由.
相关试题

