【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间. 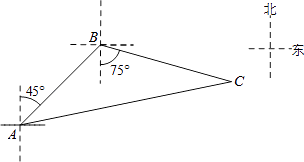
参考答案:
【答案】解:设巡逻船从出发到成功拦截所用时间为x小时;如图所示, 
由题意得:∠ABC=45°+75°=120°,AB=12,BC=10x,AC=14x,
过点A作AD⊥CB的延长线于点D,
在Rt△ABD中,AB=12,∠ABD=60°,
∴BD=ABcos60°= ![]() AB=6,AD=ABsin60°=6
AB=6,AD=ABsin60°=6 ![]() ,
,
∴CD=10x+6.
在Rt△ACD中,由勾股定理得: ![]() ,
,
解得: ![]() (不合题意舍去).
(不合题意舍去).
答:巡逻船从出发到成功拦截所用时间为2小时
【解析】设巡逻船从出发到成功拦截所用时间为x小时,由题意得出∠ABC=120°,AB=12,BC=10x,AC=14x,过点A作AD⊥CB的延长线于点D,在Rt△ABD中,由三角函数得出BD、AD的长度,得出CD=10x+6.在Rt△ACD中,由勾股定理得出方程,解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同.他们将一头骆驼前两昼夜的体温变化情况绘制成下图.请根据图像回答问题:
(1)第一天中,在什么时间范围内这头骆驼的体温是上升的?它的体温从最低上升到最高需要多少时间?
(2)第三天12时这头骆驼的体温约是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
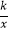 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B(  ,n).
,n). 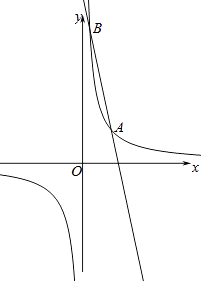
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=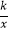 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的进度均保持不变).储运部库存物资w(吨)与时间t(小时)之间的函数关系如图所示,请问这批物资从开始调进到全部调出需要多长时间?

-
科目: 来源: 题型:
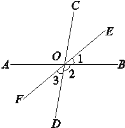
查看答案和解析>>【题目】如图,直线AB,CD交于点O,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.
(1)求∠2和∠3的度数;
(2)OF平分∠AOD吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 在平面直角坐标系
在平面直角坐标系 中的位置如图所示.
中的位置如图所示.(1)作
 关于点
关于点 成中心对称的
成中心对称的 .
.(2)将
 向右平移4个单位,作出平移后的
向右平移4个单位,作出平移后的 .
.(3)在
 轴上求作一点
轴上求作一点 ,使
,使 的值最小
的值最小 
相关试题

