Question

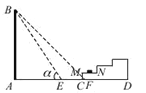
【题目】如图所示，一幢楼房AB背后有一台阶CD，台阶每层高0.2米，且AC=17.2米，设太阳光线与水平地面的夹角为α，当α=60°时，测得楼房在地面上的影长AE=10米，现有一只小猫睡在台阶的MN这层上晒太阳．（取1.73）

（1）求楼房的高度约为多少米？

（2）过了一会儿，当α=45°时，问小猫能否还晒到太阳？请说明理由．

Answer 1

【答案】（1）楼房的高度约为17.3米.（2）小猫仍可晒到太阳.理由见解析.

【解析】试题分析：（1）在Rt△ABE中，根据的正切值即可求得楼高；（2）当时，从点B射下的光线与地面AD的交点为F,与MC的交点为点H.可求得AF=AB=17.3米，又因CF=CH=17.3-17.2=0.1米，CM=0.2，所以大楼的影子落在台阶MC这个侧面上.即小猫仍可晒到太阳.

试题解析：解：（1）当当时，在Rt△ABE中，

∵,

∴BA=10tan60°=米.

即楼房的高度约为17.3米.

当时，小猫仍可晒到太阳.理由如下：

假设没有台阶，当时，从点B射下的光线与地面AD的交点为F,与MC的交点为点H.

∵∠BFA=45°，

∴,此时的影长AF=BA=17.3米，

所以CF=AF-AC=17.3-17.2=0.1.

∴CH=CF=0.1米，

∴大楼的影子落在台阶MC这个侧面上.

∴小猫仍可晒到太阳.