【题目】如图所示，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点，其顶点为D，连接AD，点P是线段AD上一个动点（不与A、D重合），过点P作y轴的垂线，垂足点为E，连接AE．

（1）求抛物线的函数解析式，并写出顶点D的坐标；

（2）如果P点的坐标为（x，y），△PAE的面积为S，求S与x之间的函数关系式，直接写出自变量x的取值范围，并求出S的最大值；

（3）在（2）的条件下，当S取到最大值时，过点P作x轴的垂线，垂足为F，连接EF，把△PEF沿直线EF折叠，点P的对应点为点P′，求出P′的坐标，并判断P′是否在该抛物线上．

参考答案：

【答案】(1)、y=﹣x2﹣2x+3；D(-1，4)；(2)、S﹣x2﹣3x（﹣3＜x＜﹣1），当x=﹣时，S取最大值；(3)、∴P′（，），不在抛物线上

【解析】

试题分析：(1)、由抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点，则代入求得a，b，c，进而得解析式与顶点D．(2)、由P在AD上，则可求AD解析式表示P点．由S△APE=PEyP，所以S可表示，进而由函数最值性质易得S最值．(3)、由最值时，P为（﹣，3），则E与C重合．画示意图，P'过作P'M⊥y轴，设边长通过解直角三角形可求各边长度，进而得P'坐标．判断P′是否在该抛物线上，将xP'坐标代入解析式，判断是否为yP'即可．

试题解析：(1)、∵抛物线y=ax2+bx+c经过A（﹣3，0）、B（1，0）、C（0，3）三点，

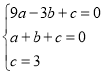∴， 解得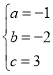：， ∴解析式为y=﹣x2﹣2x+3

∵﹣x2﹣2x+3=﹣（x+1）2+4， ∴抛物线顶点坐标D为（﹣1，4）．

(2)、∵A（﹣3，0），D（﹣1，4）， ∴设AD为解析式为y=kx+b，有， 解得，

∴AD解析式：y=2x+6， ∵P在AD上， ∴P（x，2x+6），

∴S△APE=PEyP=（﹣x）（2x+6）=﹣x2﹣3x（﹣3＜x＜﹣1），当x=﹣时，S取最大值．

(3)、如图1，设P′F与y轴交于点N，过P′作P′M⊥y轴于点M，

∵△PEF沿EF翻折得△P′EF，且P（﹣，3）， ∴∠PFE=∠P′FE，PF=P′F=3，PE=P′E=，

∵PF∥y轴， ∴∠PFE=∠FEN， ∵∠PFE=∠P′FE， ∴∠FEN=∠P′FE， ∴EN=FN，

设EN=m，则FN=m，P′N=3﹣m． 在Rt△P′EN中， ∵（3﹣m）2+（）2=m2， ∴m=．

∵S△P′EN=P′NP′E=ENP′M， ∴P′M=． 在Rt△EMP′中

∵EM=， ∴OM=EO﹣EM=， ∴P′（，）．

当x=时，y=﹣（）2﹣2+3=0.39≠， ∴点P′不在该抛物线上．

关闭