【题目】如图,Rt△ABC中,∠C=90o,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
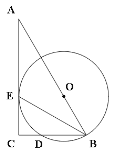
(1)求证:BE平分∠ABC;
(2)若CD︰BD=1︰2,AC=4,求CD的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
试题分析:(1)连接OE,根据OE=OB得出∠OEB=∠OBE,根据AC为切线得出∠OEA=90°,则∠C=∠OEA,从而得出OE∥BC,则∠OEB=∠EBC,从而得出∠OBE=∠EBC,得出角平分线;(2)过O作OF⊥BC于点F,连接OD,根据OD=OB,从而得出DF=BF,根据CD:BD=1:2,从而得出CD=DF=FB,从而得出四边形OECF为矩形,则CF=EO,从而得出△ODB为等边三角形,然后根据AC的长度得出BC的长度,从而得出CD的长度.
试题解析:(1)连接OE ∵OE=OB ∴∠OEB=∠OBE ∵AC与⊙O相切 ∴OE⊥AC,即∠OEA=90°
∴∠C=∠OEA=90° ∴OE∥BC ∴∠OEB=∠EBC ∴∠OBE=∠EBC 即BE平分∠ABC
(2)过O作OF⊥BC于点F,连接OD ∵OD=OB ∴DF=BF ∵CD︰BD=1︰2 ∴CD=DF=FB
∵四边形OECF为矩形 ∴CF=EO ∴OE=BD=OD=OB ∴△ODB为等边三角形 ∴∠ABC=60°
∵AC=4 ∴BC=![]() ∴CD=
∴CD=![]() ×BC=
×BC=![]()
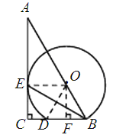
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是( )
A.对角线互相垂直平分的四边形是菱形
B.平行四边形的对角线互相平分
C.矩形的对角线相等
D.对角线相等的四边形是矩形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.

(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2﹣8x+m能配成完全平方式,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2﹣12x+a 2 是完全平方的展开式,则a的值等于_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内分解因式:a x 4﹣16a =______________ .
相关试题

