【题目】如图,点A(-10,0),B(-6,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(8,0)出发,沿x轴向左以每秒1个单位长的速度向点A匀速运动,运动时间为t秒.

(1)求点C的坐标.
(2)当∠BCP=15°时,求t的值.
(3)以PC为直径作圆,当该圆与四边形ABCD的边(或边所在的直线)相切时,求t的值.
参考答案:
【答案】(1)C(0,6);(2)8+2![]() 或8+6
或8+6![]() ;(3)2或8或17.1
;(3)2或8或17.1
【解析】
试题分析:(1)根据∠BOC=90°,∠CBO=45°得出∠BCO=∠CBO=45°,从而得出点C的坐标;(2)根据当点P在点B右侧和当点P在点B左侧两种情况分别进行计算,得出答案;(3)根据圆与BC相切、圆与CD相切和圆与AD相切三种情况分别进行计算,得出答案.
试题解析:(1)∵∠BOC=90°,∠CBO=45°,∴∠BCO=∠CBO=45°,
∵B(-6,0),∴OC=OB=6,∴C(0,6);
(2)①当点P在点B右侧时,∵∠BCO=45°,∠BCP=15°,∴∠POC=30°,
∴OP=2![]() ∴t1=8+2
∴t1=8+2![]()
②当点P在点B左侧时,∵∠BCO=45°,∠BCP=15°,∴∠POC=60°,
∴OP=6![]() ∴t2=8+6
∴t2=8+6![]()
综上所述:t的值为8+2![]() 或8+6
或8+6![]() .
.
(3)由题意知,若该圆与四边形ABCD的边相切,有以下三种情况:
①当该圆与BC相切于点C时,有∠BCP=90°, 从而∠OCP=45°,得到OP=6,此时PQ=2,∴t=2;
②当该圆与CD相切于点C时,有PC⊥CD,即点P与点O重合, 此时PQ=8,∴t=8;
③当该圆与AD相切时,设P(8-t,0),设圆心为M,则M(![]() ,3),半径r=
,3),半径r=![]()
作MH⊥AD于点H,则MH=![]() -(-10)=14-
-(-10)=14-![]() ,
,
当MH2=r2时,得(14-![]() )2=(
)2=(![]() )2+32,解得t=17.1
)2+32,解得t=17.1
∴t的值为2或8或17.1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置.设BC=2,AC=2
 ,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是 .
,则顶点A运动到点A″的位置时,点A经过的路线与直线l所围成的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是( )
A.对角线互相垂直平分的四边形是菱形
B.平行四边形的对角线互相平分
C.矩形的对角线相等
D.对角线相等的四边形是矩形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.

(1)求抛物线的解析式;
(2)求点D的坐标;
(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90o,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
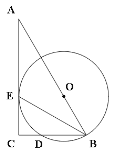
(1)求证:BE平分∠ABC;
(2)若CD︰BD=1︰2,AC=4,求CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2﹣8x+m能配成完全平方式,那么m的值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若4x2﹣12x+a 2 是完全平方的展开式,则a的值等于_________.
相关试题

