【题目】如图,在△ABC中,∠C=120°,AB=4cm,两等圆⊙A与⊙B外切,则图中两个扇形(即阴影部分)的面之和为cm2 . (结果保留π).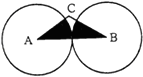
参考答案:
【答案】![]() π
π
【解析】解:∵两等圆⊙A与⊙B外切, 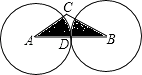
∴AD=BD= ![]() AB=2,
AB=2,
∵∠C=120°
∴∠CAB+∠CBA=60°
设∠CAB=x°,∠CBA=y°
则x+y=60
∴图中两个扇形(即阴影部分)的面积之和为 ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() π,
π,
所以答案是: ![]() π.
π.
【考点精析】关于本题考查的三角形的内角和外角和相切两圆的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;如果两圆相切,那么切点一定在连心线上,它们是轴对称图形,对称轴是两圆的连心线才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,点M、N分别表示数m,n. 则点M,N 之间的距离为|m-n|.已知点A,B,C,D在数轴上分别表示的数为a,b,c,d.且|a-c|=|b-c|=
 |d-a|=1 (a≠b),则线段BD的长度为( )
|d-a|=1 (a≠b),则线段BD的长度为( )A.3.5B.0.5C.3.5或0.5D.4.5或0.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)-23×(1-
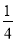 )÷0.5;
)÷0.5;(2)(
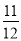 -
-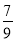 -
-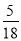 )÷
)÷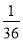 -2;
-2;(3)3(20-y)=6y-4(y-11);
(4)
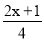 -1=
-1=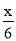 -
-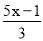 .
. -
科目: 来源: 题型:
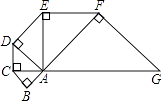
查看答案和解析>>【题目】如图,已知等腰Rt△ABC的直角边为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边.画第三个Rt△ADE,…,依此类推直到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为 .
-
科目: 来源: 题型:
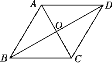
查看答案和解析>>【题目】如图,要使平行四边形ABCD是正方形,则应添加的一组条件是______(添加一组条件即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角之差的绝对值等于60°,则称这两个角互为“互优角”,(本题中所有角都是指大于0°且小于180°的角).
(1)若∠1和∠2互为“互优角”,当∠1=90°时,则∠2=_____°;
(2)如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为“互优角”,求∠BPE的度数;
(3)再将纸片沿着PF对折(点F在线段CD或AD上)使点C落在C′:
①如图2,若点E、C′、P在同一直线上,且
 与
与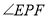 互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);②若∠B′PC′与∠EPF互为“互优角”,则∠BPE求∠CPF应满足什么样的数量关系(直接写出结果即可).

相关试题

