【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 于点
于点![]() ,点
,点![]() 为直线
为直线![]() 上不与点
上不与点![]() 重合的一个动点.
重合的一个动点.
(1)求线段![]() 的长;
的长;
(2)当![]() 的面积是6时,求点
的面积是6时,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,若存在,请直接写出所有符合条件的点
全等,若存在,请直接写出所有符合条件的点![]() 的坐标,否则,说明理由.
的坐标,否则,说明理由.

参考答案:
【答案】(1)![]() ; (2) (-4,6); (3) (
; (2) (-4,6); (3) (![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)先求得点A、B的坐标,可求得OA、OB、AB的长,利用面积法即可求得OM的长;
(2)先画图,确定△BOP面积可以BO为底,P到y轴距离为高求得P到y轴距离,再分类讨论求得答案;
(3)分△OMP≌△PQO与△OMP≌△OQP两种情况讨论,结合图象分析即可求解.
(1)对于直线![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
点A、B的坐标分别是(4,0),(0,3),
∴OA=4,OB=3,AB=![]() ,
,
∵![]() ,
,
∴![]() ;
;
(2)过P作PC⊥y轴于C,如图1,
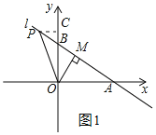
∴![]() OBPC=6,
OBPC=6,
∴PC=4,
∴点P的横坐标为4或-4,
∵点P为直线![]() 上的一个动点且不与A、B重合,
上的一个动点且不与A、B重合,
∴横坐标为4时,与A重合,不合题意,
∴横坐标为-4时,纵坐标为:![]()
∴当点P坐标为(-4,6)时,△BOP的面积是6;
(3)存在,理由如下:
①当△OMP≌△PQO时,如图2和图3,
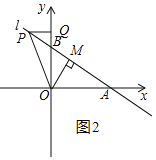
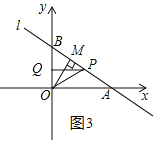
由(1)得![]() ,
,
∴PQ=OM=![]() ,即P点横坐标为
,即P点横坐标为![]() 或
或![]() ,
,
纵坐标为:![]() 或
或![]() ,
,
此时点P的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);
②当△OMP≌△OQP时,如图4和图5,
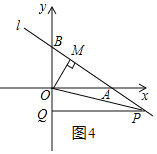
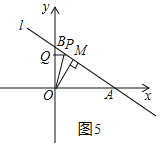
∴OQ=OM=![]() ,即即点P、点Q纵坐标为
,即即点P、点Q纵坐标为![]() 或
或![]() ,
,
由![]() ,解得:
,解得:![]() ;
;
由![]() ,解得:
,解得:![]() ;
;
此时点P的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() );
);
综上所述,符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) .
) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2
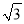 , 求AE.
, 求AE.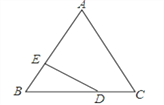
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题呈现:我们知道反比例函数y=
 (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y= +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y= (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=
 的图象.
的图象.(1)填写下表,并画出函数y=
 的图象.
的图象.①列表:
x
…
﹣5
﹣3
﹣2
0
1
3
…
y
…
…
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=
 的图象是由函数y=
的图象是由函数y= 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .灵活应用:根据上述画函数图象的经验,想一想函数y=
 +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小敏在测量学校一幢教学楼AB的高度时,她先在点C测得教学楼的顶部A的仰角为30°,然后向教学楼前进12米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.
(结果精确到0.1米,参考数据:
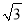 ≈1.73)
≈1.73)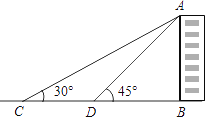
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度
1:20
1:16
1:12
最大高度(米)
1.50
1.00
0.75
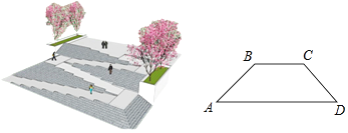
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )


A.6B.
 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个转盘分成六等份,依次标上数字1、2、3、4、5、6,小明和小芳分别只转动一次转盘.小明同学先转动转盘,结果指针指向2,接下来小芳转动转盘,若把小明和小芳转动转盘指针指向的数字分别记作
 、
、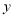 ,把
,把 、
、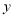 作为点
作为点 的横、纵坐标.
的横、纵坐标.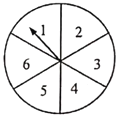
(1)写出点
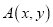 所有可能的坐标;
所有可能的坐标;(2)求点
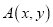 在直线
在直线 上的概率.
上的概率.
相关试题

