搜索
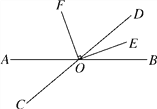
【题目】如图，已知直线AB与CD相交于点O，OE是∠BOD的平分线，OF⊥OE，∠BOE＝20°.
(1)求∠AOC的度数；
(2)求∠COF的度数．
参考答案：
【答案】（1）40°；（2）110°.
【解析】试题分析：（1）根据角平分线的性质可得∠DOE=∠BOE=
∠BOD，再由∠BOE=20°可得∠BOD的度数，然后再根据对顶角相等可得答案；
（2）根据垂直定义可得∠EOF=90°，再利用平角定义计算出∠AOF的度数，然后可得∠COF的度数．
试题解析：
（1）∵OE是∠BOD的平分线，
∴∠DOE=∠BOE=
∠BOD，
∵∠BOE=20°，
∴∠BOD=40°，
∴∠AOC=40°；
（2）∵EO⊥FO于O，
∴∠EOF=90°，
∵∠BOE=20°，
∴∠AOF=180°-90°-20°=70°，
∴∠COF=70°+40°=110°．
-
科目： 来源： 题型：
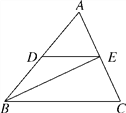
查看答案和解析>>【题目】如图，已知DE∥BC，BE平分∠ABC，∠C＝65°，∠ABC＝50°.
(1)求∠BED的度数；
(2)判断BE与AC的位置关系，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分10分）
【感受联系】在初二的数学学习中，我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形，直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系，发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程，请你补充完整证明过程
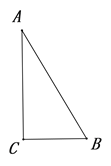
已知：如图，在
△
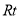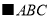中， 
°，
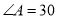°.求证：
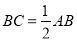．证明：
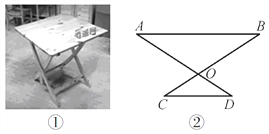
【灵活运用】该同学家有一张折叠方桌如图①所示，方桌的主视图如图②.经测得
， 
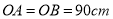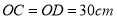，将桌子放平，两条桌腿叉开的角度
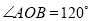.求：桌面与地面的高度．
-
科目： 来源： 题型：
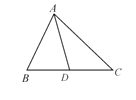
查看答案和解析>>【题目】如图所示，AD是△ABC的边BC的中线.
(1)画出以点D为对称中心，与△ABD成中心对称的三角形；
(2)若AB=10，AC=12，求AD长的取值范围.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商家预测一种应季衬衫能畅销市场，就用13 200元购进了一批这种衬衫，面市后果然供不应求，商家又用28 800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．
(1)该商家购进的第一批衬衫是多少件？
(2)若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完利润率不低于25%(不考虑其他因素)，那么每件衬衫的标价至少是多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，并完成填空．
你能比较20152 016和20162 015的大小吗？
为了解决这个问题，先把问题一般化，比较nn＋1和(n＋1)n(n≥1，且n为整数)的大小．然后从分析n＝1，n＝2，n＝3…的简单情形入手，从中发现规律，经过归纳、猜想得出结论．
(1)通过计算(可用计算器)比较下列①～⑦组两数的大小：(在横线上填上“>”“＝”或“<”)
①12____21；②23_____32；③34_____43；④45_____54；
⑤56____65；⑥67_____76；⑦78_____87；
(2)归纳第(1)问的结果，可以猜想出nn＋1和(n＋1)n的大小关系；
(3)根据以上结论，可以得出20162017和20172016的大小关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面内，正方形ABCD与正方形CEFH如图放置，连接DE，BH，两线交于M，求证：
（1）BH＝DE；
（2）BH⊥DE．
相关试题
