【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= ![]() b2+
b2+ ![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴ ![]() b2+
b2+ ![]() ab=
ab= ![]() c2+
c2+ ![]() a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 . 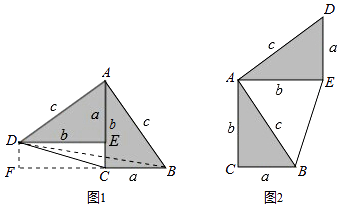
参考答案:
【答案】证明:连结BD,过点B作DE边上的高BF,则BF=b﹣a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE= ![]() ab+
ab+ ![]() b2+
b2+ ![]() ab,
ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE= ![]() ab+
ab+ ![]() c2+
c2+ ![]() a(b﹣a),
a(b﹣a),
∴ ![]() ab+
ab+ ![]() b2+
b2+ ![]() ab=
ab= ![]() ab+
ab+ ![]() c2+
c2+ ![]() a(b﹣a),
a(b﹣a),
∴a2+b2=c2 . 
【解析】首先连结BD,过点B作DE边上的高BF,则BF=b﹣a,表示出S五边形ACBED , 两者相等,整理即可得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)在Rt
 中,
中, 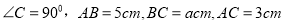 且
且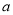 是方程
是方程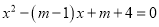 的根.
的根.(1)求
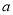 和
和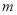 的值;
的值;(2)如图(2),有一个边长为
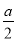 的等边三角形
的等边三角形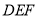 从
从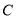 出发,以1厘米每秒的速度沿
出发,以1厘米每秒的速度沿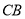 方向移动,至
方向移动,至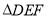 全部进入与
全部进入与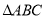 为止,设移动时间为xs,
为止,设移动时间为xs, 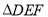 与
与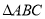 重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;
重叠部分面积为y,试求出y与x的函数关系式并注明x的取值范围;(3)试求出发后多久,点
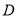 在线段
在线段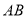 上?
上?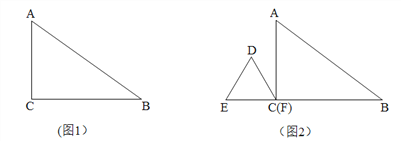
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果tanα=0.213,那么锐角α的度数大约为( )
A.8°
B.10°
C.12°
D.15° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B都在数轴上,且AB=6
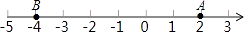
(1)点B表示的数是;
(2)若点B以每秒2个单位的速度沿数轴向右运动,则2秒后点B表示的数是;
(3)若点A、B都以每秒2个单位沿数轴向右运动,而点O不动,t秒后有一个点是一条线段的中点,求t. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)如图,在直线m的同侧有A,B两点,在直线m上找点P,Q,使PA+PB最小,|QB﹣QA|最大(保留作图痕迹)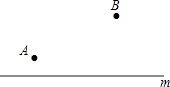
(2)平面直角坐标系内有两点A(2,3),B(4,5),请分别在x轴,y轴上找点P,Q,使PA+PB最小,|QB﹣QA|最大,则点P,Q的坐标分别为 ,
(3)代数式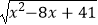 +
+ 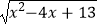 的最小值是 , 此时x=
的最小值是 , 此时x=
(4)代数式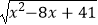 ﹣
﹣ 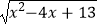 的最大值是 , 此时x= .
的最大值是 , 此时x= . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中与多项式2x﹣3y+4z相等的是( )
A.2x+(3y﹣4z)
B.2x﹣(3y﹣4z)
C.2x+(3y+4z)
D.2x﹣(3y+4z) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣4﹣28﹣(﹣19)+(﹣24)
(2)(﹣ )﹣(﹣1
)﹣(﹣1  )﹣(﹣1
)﹣(﹣1  )﹣(+1.75).
)﹣(+1.75).
(3)( +
+ 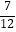 ﹣
﹣  )×(﹣60)
)×(﹣60)
(4)﹣14﹣ ×[1﹣(﹣3)2].
×[1﹣(﹣3)2].
相关试题

