搜索
【题目】计算
（1）﹣4﹣28﹣（﹣19）+（﹣24）
（2）（﹣ 
）﹣（﹣1 
）﹣（﹣1 ）﹣（+1.75）．
（3）（ + 
﹣ 
）×（﹣60）
（4）﹣14﹣ 
×[1﹣（﹣3）2]．
参考答案：
【答案】
（1）解：原式=﹣4﹣28+19﹣24=（﹣4﹣28﹣24）+19=﹣56+19=﹣37
（2）解：原式=﹣ 
+1 +1 
﹣1.75=1
（3）解：原式=﹣45﹣35+70=﹣80+70=﹣10
（4）解：原式=﹣1﹣ 
×（﹣8）=﹣1+ 
= 
【解析】（1）原式利用减法法则变形，计算即可得到结果；（2）原式利用减法法则变形，计算即可得到结果；（3）原式利用乘法分配律计算即可得到结果；（4）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果．
【考点精析】解答此题的关键在于理解有理数的四则混合运算的相关知识，掌握在没有括号的不同级运算中，先算乘方再算乘除，最后算加减．
-
科目： 来源： 题型：
查看答案和解析>>【题目】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：
将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2
证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=
b2+ ab．
又∵S四边形ADCB=S△ADB+S△DCB= c2+ a（b﹣a）
∴ b2+ ab= c2+ a（b﹣a）
∴a2+b2=c2
请参照上述证法，利用图2完成下面的证明．
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2 ．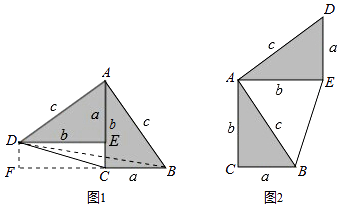
-
科目： 来源： 题型：
查看答案和解析>>【题目】解答
（1）如图，在直线m的同侧有A，B两点，在直线m上找点P，Q，使PA+PB最小，|QB﹣QA|最大（保留作图痕迹）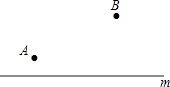
（2）平面直角坐标系内有两点A（2，3），B（4，5），请分别在x轴，y轴上找点P，Q，使PA+PB最小，|QB﹣QA|最大，则点P，Q的坐标分别为 ，
（3）代数式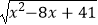
+ 
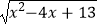的最小值是 ， 此时x=
（4）代数式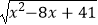 ﹣ 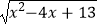的最大值是 ， 此时x= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列各式中与多项式2x﹣3y+4z相等的是（ ）
A.2x+（3y﹣4z）
B.2x﹣（3y﹣4z）
C.2x+（3y+4z）
D.2x﹣（3y+4z） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，ABCD的对角线AC、BD相交于点O，增加下列条件后，ABCD不一定是菱形的是（ ）
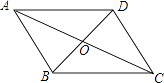
A.DC=BC
B.AC⊥BD
C.AB=BD
D.∠ADB=∠CDB -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴的原点为0，点A、B、C是数轴上的三点，点B对应的数位1，AB=6，BC=2，动点P、Q同时从A、C出发，分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动．设运动时间为t秒（t＞0）
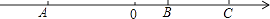
（1）求点A、C分别对应的数；
（2）求点P、Q分别对应的数（用含t的式子表示）
（3）试问当t为何值时，OP=OQ？ -
科目： 来源： 题型：
查看答案和解析>>【题目】为了解广陵区八年级学生的视力情况，在全区八年级学生中随机抽取了800名学生进行视力检查，在这个问题中样本容量是_______．
相关试题
