【题目】下列各式中与多项式2x﹣3y+4z相等的是( )
A.2x+(3y﹣4z)
B.2x﹣(3y﹣4z)
C.2x+(3y+4z)
D.2x﹣(3y+4z)
参考答案:
【答案】B
【解析】解:A、2x+(3y﹣4z)=2x+3y﹣4z,故此选项错误;
B、2x﹣(3y﹣4z)=2x﹣3y+4z,故此选项正确;
C、2x+(3y+4z)=2x+3y+4z,故此选项错误;
D、2x﹣(3y+4z)=2x﹣3y﹣4z,故此选项错误;
故选:B.
根据去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反分别把四个选项去括号,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B都在数轴上,且AB=6
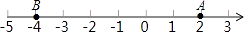
(1)点B表示的数是;
(2)若点B以每秒2个单位的速度沿数轴向右运动,则2秒后点B表示的数是;
(3)若点A、B都以每秒2个单位沿数轴向右运动,而点O不动,t秒后有一个点是一条线段的中点,求t. -
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC= b2+
b2+  ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= c2+
c2+  a(b﹣a)
a(b﹣a)
∴ b2+
b2+  ab=
ab=  c2+
c2+  a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .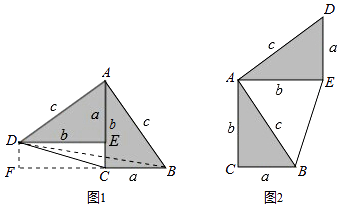
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)如图,在直线m的同侧有A,B两点,在直线m上找点P,Q,使PA+PB最小,|QB﹣QA|最大(保留作图痕迹)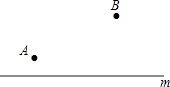
(2)平面直角坐标系内有两点A(2,3),B(4,5),请分别在x轴,y轴上找点P,Q,使PA+PB最小,|QB﹣QA|最大,则点P,Q的坐标分别为 ,
(3)代数式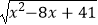 +
+ 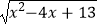 的最小值是 , 此时x=
的最小值是 , 此时x=
(4)代数式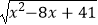 ﹣
﹣ 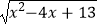 的最大值是 , 此时x= .
的最大值是 , 此时x= . -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)﹣4﹣28﹣(﹣19)+(﹣24)
(2)(﹣ )﹣(﹣1
)﹣(﹣1  )﹣(﹣1
)﹣(﹣1  )﹣(+1.75).
)﹣(+1.75).
(3)( +
+ 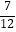 ﹣
﹣  )×(﹣60)
)×(﹣60)
(4)﹣14﹣ ×[1﹣(﹣3)2].
×[1﹣(﹣3)2]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,增加下列条件后,ABCD不一定是菱形的是( )
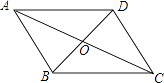
A.DC=BC
B.AC⊥BD
C.AB=BD
D.∠ADB=∠CDB -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴的原点为0,点A、B、C是数轴上的三点,点B对应的数位1,AB=6,BC=2,动点P、Q同时从A、C出发,分别以每秒2个长度单位和每秒1个长度单位的速度沿数轴正方向运动.设运动时间为t秒(t>0)
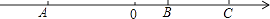
(1)求点A、C分别对应的数;
(2)求点P、Q分别对应的数(用含t的式子表示)
(3)试问当t为何值时,OP=OQ?
相关试题

