【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
参考答案:
【答案】
(1)解:设装运乙、丙水果的车分别为x辆,y辆,得:
![]() ,
,
解得: ![]() .
.
答:装运乙种水果的车有2辆、丙种水果的汽车有6辆
(2)解:设装运乙、丙水果的车分别为a辆,b辆,得:
![]() ,
,
解得 ![]() .
.
答:装运乙种水果的汽车是(m﹣12)辆,丙种水果的汽车是(32﹣2m)辆
(3)解:设总利润为w千元,
w=5×4m+7×2(m﹣12)+4×3(32﹣2m)=10m+216.
∵ 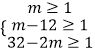 ,
,
∴13≤m≤15.5,
∵m为正整数,
∴m=13,14,15,
在w=10m+216中,w随x的增大而增大,
∴当m=15时,W最大=366(千元),
答:当运甲水果的车15辆,运乙水果的车3辆,运丙水果的车2辆,利润最大,最大利润为366千元
【解析】(1)根据“8辆汽车装运乙、丙两种水果共22吨到A地销售”列出方程组,即可解答;(2)设装运乙、丙水果的车分别为a辆,b辆,列出方程组 ![]() ,即可解答;(3)设总利润为w千元,表示出w=10m+216.列出不等式组
,即可解答;(3)设总利润为w千元,表示出w=10m+216.列出不等式组 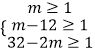 ,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
,确定m的取值范围13≤m≤15.5,结合一次函数的性质,即可解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,2),连接AB,点P是x轴上的一个动点,连接AP、BP,当△ABP的周长最小时,对应的点P的坐标和△ABP的最小周长分别为( )

A. (1,0),
 B. (3,0),
B. (3,0),  C. (2,0),
C. (2,0),  D. (2,0),
D. (2,0), 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
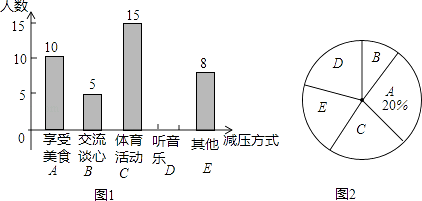
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率. -
科目: 来源: 题型:
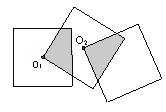
查看答案和解析>>【题目】如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
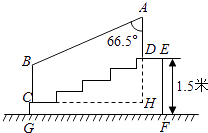
(1)求点D与点C的高度差DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米) -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
已知:两条线段
 、
、 .
.
求作:菱形
 ,使得其对角线分别等于
,使得其对角线分别等于 和
和 .
.小军的作法如下:
如图

(
 )画一条线段
)画一条线段 等于
等于 .
.(
 )分别以
)分别以 、
、 为圆心,大于
为圆心,大于 的长为半径,在线段
的长为半径,在线段 的上下各作两条弧,两弧相交于
的上下各作两条弧,两弧相交于 、
、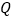 两点.
两点.(
 )作直线
)作直线 交
交 于
于 点.
点.(
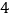 )以
)以 点为圆心,线段
点为圆心,线段 的长为半径作两条弧,交直线
的长为半径作两条弧,交直线 于
于 、
、 两点,连接
两点,连接 、
、 、
、 、
、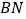 .
.所以四边形
 就是所求的菱形.
就是所求的菱形.老师说:“小军的作法正确”.
该作图的依据是__________和___________.
相关试题

