【题目】几何图形很神奇,由一些多边形组成的图形中离不开边和顶点,它们之间有着很多奥秘等待我们去探索.先看下面一道有趣的关于顶点和边的题:如图所示,图①~图④都是平面图形.

(1)每个图中各有多少个顶点?多少条边?这些边围出多少个区域?请将结果填入下列表格中:

(2)根据(1)中的结论,推断出一个平面图形的顶点数、边数、区域数之间有什么关系(设顶点数为n).
参考答案:
【答案】(1)填表见解析;(2)若顶点数为n,则边数=![]() ,区域数=
,区域数=![]() +1.
+1.
【解析】
(1)根据所给图形进行分析解答即可;
(2)根据(1)中所得表格中的数据分析找到:平面图形的顶点个数n与边数和分成的区域个数间的关系即可.
(1)
图序 | 顶点数(个) | 边数(条) | 区域数(个) |
① | 4 | 6 | 3 |
② | 6 | 9 | 4 |
③ | 8 | 12 | 5 |
④ | 10 | 15 | 6 |
(2)由(1)中所填表格中的数据可得:若顶点数为n,则边数=![]() ,区域数=
,区域数=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是生活中常见的月历表,你对它了解吗?
(1)如果下表是另一个月的月历表,a表示该月中某一天,b,c,d是该月中其他3天,那么b,c,d与a有什么关系?b=________;c=________;d=________(用含a的式子填空).

(2)用一个长方形框圈出月历表中的三个数(如上表中的阴影),若这三个数之和等于51,则这三个数各是多少?
(3)这样圈出的三个数之和可能是64吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠):

(1)填写下表:

(2)原正方形能否被分割成2018个三角形?若能,求此时正方形ABCD内部有多少个点;若不能,请说明理由.
-
科目: 来源: 题型:
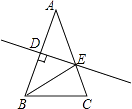
查看答案和解析>>【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A.
B.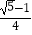
C.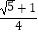
D.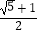
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,郑某把一块边长为a m的正方形的土地租给李某种植,他对李某说:“我把你这块地的一边减少5 m,另一边增加5 m,继续租给你,你也没有吃亏,你看如何”.李某一听,觉得自己好像没有吃亏,就答应了.同学们,你们觉得李某有没有吃亏?请说明理由.
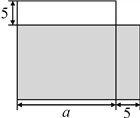
【答案】李某吃亏了,理由见解析.
【解析】试题分析:计算阴影部分面积和原正方形面积作比较.
试题解析:
解:李某吃亏了.理由如下:
∵(a+5)(a-5)=a2-25<a2,
∴李某少种了25 m2地,李某吃亏了.
【题型】解答题
【结束】
20【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有5张看上去无差别的卡片,上面分别写着1,2,3,4,5,随机抽取3张,用抽到的三个数字作为边长,恰能构成三角形的概率是( )
A.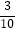 ?
?
B.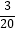 ?
?
C.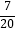 ?
?
D.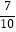
相关试题

