【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)求证:AE∥CF.
(2)BC平分∠DBE吗?为什么?

参考答案:
【答案】(1)见详解;(2)BC平分∠DBE,证明见详解.
【解析】
(1)根据同角的补角相等,证明∠2=∠DBE,问题得证;
(2)先证明AD∥BC,进而证明∠C=∠CBD,再根据AE∥CF,证明∠CBD=∠CBE,问题得证.
解:(1)证明:∵∠1+∠2=180°,∠1+∠DBE=180°,
∴∠2=∠DBE,
∴AE∥CF;
(2)BC平分∠DBE,
证明:∵AE∥CF,
∴∠C+∠CBA=180°,
∵∠A=∠C,
∴∠A+∠CBA=180°,
∴AD∥BC,
∴∠ADB=∠CBD,∠FDA=∠C,
∵DA平分∠BDF,
∴∠FDA=∠ADB,
∴∠C=∠CBD,
∵AE∥CF,
∴∠C=∠CBE,
∴∠CBD=∠CBE,
∴BC平分∠DBE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )
A.20°
B.50°
C.20°或160°
D.50°或130° -
科目: 来源: 题型:
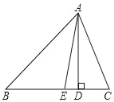
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,点E在BC上,AE是∠BAC的平分线,BE=AE,∠B=40°.
(1)求∠EAD的度数;
(2)求∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
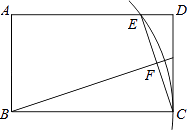
A.
B.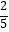
C.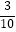
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由相同大小的△按一定规律组成的,其中第(①个图形中一共有3个△,第②个图形中一共有8个△,第③个图形中一共有14个△,…,按此规律排列下去,第⑨个图形中的△个数为( )
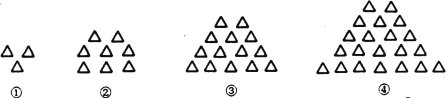
A. 54B. 61C. 71D. 77
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c,当2<x<5时,y随x的增大而减小,则实数b的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】.计算:
(1)
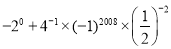
(2)(2x1)(2x1)(2x1)2
(3)(a3b2c)(a3b2c)
(4)10397(运用公式简算)
相关试题

