【题目】已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )
A.20°
B.50°
C.20°或160°
D.50°或130°
参考答案:
【答案】D
【解析】解: 
∵OA=OB,
∴∠OBA=∠OAB=40°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=100°,
∴∠ACB= ![]() ∠AOB=50°.
∠AOB=50°.
当点C在点C′的位置时,∠AC′B=180°﹣50°=130°.
所以答案是:D.
【考点精析】本题主要考查了圆周角定理和圆内接四边形的性质的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点B(a,b)是第一象限内一点,且a、b满足等式a2-6a+9+|b-1|=0.

(1)求点B的坐标;
(2)如图,动点C以每秒1个单位长度的速度从O点出发,沿x轴的正半轴方向运动,同时动点A以每秒2个单位长度的速度从O点出发,沿y轴的正半轴方向运动,设运动的时间为t秒,当t为何值时,△ABC是AB为斜边的等腰直角三角形;
(3)如图,在(2)的条件下,作∠ABC的平分线BD,设BD的长为m,△ADB的面积为S.请用含m的式子表示S.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为8的等边三角形ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度每秒1个单位长度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.
(1)当DF⊥AB时,求AD的长;
(2)求证:EG=
 AC.
AC.(3)点D从A出发,经过几秒,CG=1.6?直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元
 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同. 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价; 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件? -
科目: 来源: 题型:
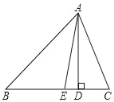
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,点E在BC上,AE是∠BAC的平分线,BE=AE,∠B=40°.
(1)求∠EAD的度数;
(2)求∠C的度数.
-
科目: 来源: 题型:
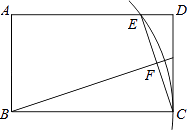
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
A.
B.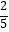
C.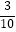
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)求证:AE∥CF.
(2)BC平分∠DBE吗?为什么?

相关试题

