【题目】关于二次函数y=﹣2x2+1,下列说法错误的是( )
A.图象开口向下
B.图象的对称轴为x= ![]()
C.函数最大值为1
D.当x>1时,y随x的增大而减小
参考答案:
【答案】B
【解析】解: ∵y=﹣2x2+1,
∴抛物线开口向下,故A正确;对称轴为x=0,故B不正确;函数有最大值1,故C正确;
当x>0时,y随x的增大而减小,故D正确;
故选B.
【考点精析】通过灵活运用二次函数的性质和二次函数的最值,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).求:

(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离. -
科目: 来源: 题型:
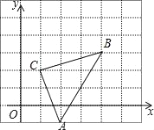
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
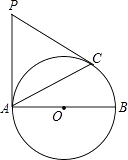
(1)求∠P的大小;
(2)若AB=6,求PA的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为 .

-
科目: 来源: 题型:
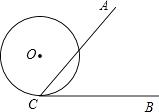
查看答案和解析>>【题目】如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离是cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,∠C=20°,AD为△ABC的高,AE为角平分线.求∠EAD的度数.

相关试题

