搜索
【题目】如图（1）是某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状．抛物线两端点与水面的距离都是1m，拱桥的跨度为10cm．桥洞与水面的最大距离是5m．桥洞两侧壁上各有一盏距离水面4m的景观灯．现把拱桥的截面图放在平面直角坐标系中，如图（2）．求： 
（1）抛物线的解析式；
（2）两盏景观灯P1、P2之间的水平距离．
参考答案：
【答案】
（1）解：抛物线的顶点坐标为（5，5），与y轴交点坐标是（0，1），
设抛物线的解析式是y=a（x﹣5）2+5，
把（0，1）代入y=a（x﹣5）2+5，
得a=﹣ 
，
∴y=﹣ （x﹣5）2+5（0≤x≤10）
（2）解：由已知得两景观灯的纵坐标都是4，
∴4=﹣ （x﹣5）2+5，
∴ （x﹣5）2=1，
∴x1= 
，x2= 
，
∴两景观灯间的距离为 ﹣ =5米
【解析】（1）由图形可知这是一条抛物线，根据图形也可以知道抛物线的顶点坐标为（5，5），与y轴交点坐标是（0，1），设出抛物线的解析式将两点代入可得抛物线方程；（2）第二题中要求灯的距离，只需要把纵坐标为4代入，求出x，然后两者相减，就是它们的距离．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为[x]．即当n为非负整数时，若n﹣
≤x＜n+ ，则[x]=n．如：[3.4]=3，[3.5]=4，…根据以上材料，解决下列问题： （1）填空：
①若[x]=3，则x应满足的条件：________；
②若[3x+1]=3，则x应满足的条件：________；
（2）求满足[x]=
x﹣1的所有非负实数x的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为＜x＞，即：当n为非负整数时，如果n﹣
≤x＜n+ ，则＜x＞=n． 如：＜0＞=＜0.48＞=0，＜0.64＞=＜1.493＞=1，＜2＞=2，＜3.5＞=＜4.12＞=4，…试解决下列问题：
（1）填空：①＜π＞=________；②如果＜2x﹣1＞=3，则实数x的取值范围为________；
（2）①当x≥0，m为非负整数时，求证：＜x+m＞=m+＜x＞；②举例说明＜x+y＞=＜x＞+＜y＞不恒成立；
（3）求满足＜x＞=
x的所有非负实数x的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】解一元二次不等式
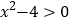．请按照下面的步骤，完成本题的解答．
解：
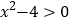可化为 
． （1）依据“两数相乘，同号得正”，可得不等式组①
或不等式组②________． （2）解不等式组①，得________．
（3）解不等式组②，得________．
（4）一元二次不等式
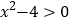的解集为________． -
科目： 来源： 题型：
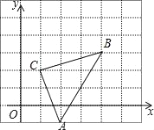
查看答案和解析>>【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）
（1）写出点A、B的坐标：A（ ， ）、B（ ， ）
（2）将△ABC先向左平移1个单位长度，再向上平移2个单位长度，得到△A′B′C′，画出△A′B′C′
（3）写出三个顶点坐标A′（ 、 ）、B′（ 、 ）、C′ ( 、 ）
（4）求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，AB为⊙O的直径，PA，PC是⊙O的切线，A，C为切点，∠BAC=30°．
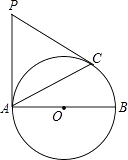
（1）求∠P的大小；
（2）若AB=6，求PA的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】关于二次函数y=﹣2x2+1，下列说法错误的是（ ）
A.图象开口向下
B.图象的对称轴为x=
C.函数最大值为1
D.当x＞1时，y随x的增大而减小
相关试题
