【题目】如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以![]() 个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以![]() 个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
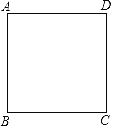
A. 点AB. 点BC. 点CD. 点D
参考答案:
【答案】D
【解析】
设两只电子蚂蚁每隔x秒相遇一次,根据正方形周长=二者速度之和×时间,可得出关于x的一元一次方程,解之即可得出两只电子蚂蚁每隔2秒相遇一次,再结合电子蚂蚁Q的速度、出发点及运动方向可得出它们第1次、第2次、第3次、第4次、第5次……相遇点,结合2019÷4=504……3可得出结论.
解:设两只电子蚂蚁每隔x秒相遇一次,
根据题意得:(![]() +
+![]() )x=1×4,
)x=1×4,
解得:x=2.
∵电子蚂蚁Q从点A出发,以![]() 个单位长度/秒的速度绕正方形作逆时针运动,
个单位长度/秒的速度绕正方形作逆时针运动,
∴它们第1次相遇在B点,第2次相遇在C点,第3次相遇在D点,第4次相遇在A点,第5次相遇在B点,第6次相遇在C点,….
又∵2019÷4=504……3,
∴第2019次相遇和第3次相遇地点相同,即第2019次相遇在点D.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】拖拉机油箱储油60.5
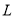 ,在正常情况下,拖拉机工作1
,在正常情况下,拖拉机工作1 耗油5.5
耗油5.5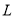 ,
,(1)工作
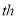 后油箱内还剩多少
后油箱内还剩多少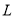 油?
油?(2)利用(1)的结果分别计算拖拉机工作4.5
 ,6
,6 后油箱内剩油量;
后油箱内剩油量;(3)这台拖拉机最多能工作多少
 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和一体机,经过市场考察得知,购进 1 台笔记本电脑和 2 台一体机需要 1.45 万元,购进 2 台笔记本电脑和 1 台一体机需要 1.55 万元.
(1)求每台笔记本电脑、一体机各多少万元?
(2)根据学校实际,需购进笔记本电脑和一体机共35台,总费用不超过17.5万元,但不低于 17.2万元,请你通过计算求出共几种购买方案,并写出费用最低具体方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x,y 的二元一次方程组
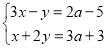 的解都是正数.
的解都是正数. (1)求a的取值范围;
(2)化简:
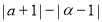 ;
; (3)若上述二元一次方程组的解是一个等腰三角形的一条腰和底边的长,且这个等腰三角形的周长为12,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为1,在方格纸内将
 经过一次平移后得到
经过一次平移后得到 ,图中标出了点
,图中标出了点 的对应点
的对应点 ,利用网格点和三角板画图或计算:
,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的
 .
.(2)画出
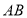 边的中线
边的中线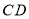 .
.(3)画出
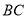 边的高线
边的高线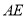 .
.(4)
 的面积为 .
的面积为 .(5)在图中能使
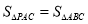 的格点
的格点 的个数有 个 (点
的个数有 个 (点 异于点
异于点 ).
). -
科目: 来源: 题型:
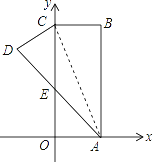
查看答案和解析>>【题目】如图,在直角坐标系中,长方形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(2,6),将长方形沿对角线AC翻折,点B落在点D的位置,且AD交y轴于点E,则点D的坐标为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
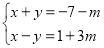 的解满足
的解满足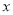 为非正数,
为非正数,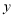 为负数.
为负数.(1)求
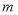 的取值范围
的取值范围(2)在(1)的条件下,若不等式
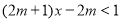 的解为
的解为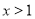 ,求整数
,求整数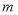 的值.
的值.
相关试题

