【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和一体机,经过市场考察得知,购进 1 台笔记本电脑和 2 台一体机需要 1.45 万元,购进 2 台笔记本电脑和 1 台一体机需要 1.55 万元.
(1)求每台笔记本电脑、一体机各多少万元?
(2)根据学校实际,需购进笔记本电脑和一体机共35台,总费用不超过17.5万元,但不低于 17.2万元,请你通过计算求出共几种购买方案,并写出费用最低具体方案.
参考答案:
【答案】(1)每台笔记本电脑0.55万元,每台一体机0.45万元;(2)购买电脑15台,电子白板20台最省钱.
【解析】
(1)先设每台电脑x万元,每台一体机y万元,根据购进1台笔记本电脑和2台一体机需要1.45万元,购进2台笔记本电脑和1台一体机需要1.55万元,列出方程组,求出x,y的值即可;
(2)设需购进笔记本电脑a台,则购进一体机(35-a)台,根据需购进笔记本电脑和一体机共35台,总费用不超过19万元,但不低于17万元,列出不等式组,求出a的值,再根据每台电脑的价格和一体机的价格,算出总费用,再进行比较,即可得出最省钱的方案.
解:(1)设每台笔记本电脑x万元,每台一体机y万元,根据题意得:
![]() ,
,
解得:![]() ,
,
答:每台笔记本电脑0.55万元,每台一体机0.45万元.
(2)设需购进笔记本电脑a台,则购进一体机(35-a)台,根据题意得:
![]() ,
,
解得:14.5≤a≤17.5,
∵a为正整数,
∴a=15、16、17.
∴共有三种方案:
方案一:购进笔记本电脑15台,一体机20台,总费用为15×0.55+20×0.45=17.25(万元);
方案二:购进笔记本电脑16台,一体机19台,总费用为16×0.55+19×0.45=17.35(万元),
方案三:购进笔记本电脑17台,一体机18台,17×0.55+18×0.45=17.45(万元);
∵17.25<17.35<17.45,
∴选择方案三最省钱,即购买电脑15台,电子白板20台最省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN。其中正确的结论有( )
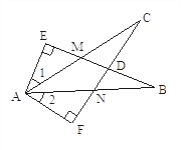
A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, DE AB 于 E , DF AC 于 F ,若 BD CD 、 BE CF ,
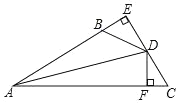
(1)求证:AD平分BAC ;
(2)已知AC 14,BE 2,求AB的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】拖拉机油箱储油60.5
 ,在正常情况下,拖拉机工作1
,在正常情况下,拖拉机工作1 耗油5.5
耗油5.5 ,
,(1)工作
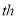 后油箱内还剩多少
后油箱内还剩多少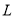 油?
油?(2)利用(1)的结果分别计算拖拉机工作4.5
 ,6
,6 后油箱内剩油量;
后油箱内剩油量;(3)这台拖拉机最多能工作多少
 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x,y 的二元一次方程组
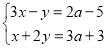 的解都是正数.
的解都是正数. (1)求a的取值范围;
(2)化简:
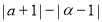 ;
; (3)若上述二元一次方程组的解是一个等腰三角形的一条腰和底边的长,且这个等腰三角形的周长为12,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,电子蚂蚁P、Q在边长为1个单位长度的正方形ABCD的边上运动,电子蚂蚁P从点A出发,以
 个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以
个单位长度/秒的速度绕正方形作顺时针运动,电子蚂蚁Q从点A出发,以 个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )
个单位长度秒的速度绕正方形作逆时针运动,则它们第2019次相遇在( )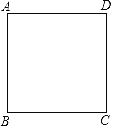
A. 点AB. 点BC. 点CD. 点D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都为1,在方格纸内将
 经过一次平移后得到
经过一次平移后得到 ,图中标出了点
,图中标出了点 的对应点
的对应点 ,利用网格点和三角板画图或计算:
,利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的
 .
.(2)画出
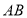 边的中线
边的中线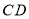 .
.(3)画出
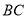 边的高线
边的高线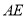 .
.(4)
 的面积为 .
的面积为 .(5)在图中能使
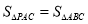 的格点
的格点 的个数有 个 (点
的个数有 个 (点 异于点
异于点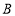 ).
).
相关试题

